Comparison with Kaplansky's solution
Next: Conclusion
Up: Non-sexist solution of the
Previous: Solution to the
The solution that we have just given is completely straight-forward
and elementary, yet we have said that the ménage problem is still
generally regarded to be tricky. How can this be? The answer can be
given in two words: ``Ladies first.'' It apparently never occurred to
anyone who looked at the problem not to seat the ladies first (or in a
few cases, the gentlemen). Thus Kaplansky and Riordan
16]
:
``We may
begin by fixing the position of husbands or wives, say wives for
courtesy's sake.''
Seating the ladies first ``reduces'' the ménage problem to a problem
of permutations with restricted position. Unfortunately, this new
problem is more difficult
than the problem we began with, as we may judge from the
cleverness of Kaplansky's solution
[5]:
We now restate the problème des ménages in the usual fashion by
observing that the answer is 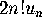 , where
, where 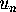 is the number of
permutations of
is the number of
permutations of 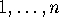 which do not satisfy any of the following
which do not satisfy any of the following
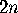 conditions: 1 is 1st or 2nd, 2 is 2nd or 3rd,...,
conditions: 1 is 1st or 2nd, 2 is 2nd or 3rd,...,  is
is  th or 1st.
Now let us select a subset of
th or 1st.
Now let us select a subset of 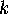 conditions from the above
conditions from the above 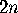 and
inquire how many permutations of
and
inquire how many permutations of 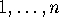 there are which satisfy
all
there are which satisfy
all 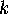 ; the answer is
; the answer is 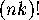 or 0 according as the
or 0 according as the 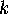 conditions are
compatible or not. If we further denote by
conditions are
compatible or not. If we further denote by 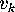 the number of ways of
selecting
the number of ways of
selecting 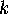 compatible conditions from the
compatible conditions from the 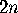 , we have, by the
familiar argument of inclusion and exclusion,
, we have, by the
familiar argument of inclusion and exclusion,  .
It remains to evaluate
.
It remains to evaluate 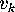 , for which purpose we note that the
, for which purpose we note that the 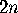 conditions, when arrayed in a circle, have the property that only
consecutive ones are not compatible....
conditions, when arrayed in a circle, have the property that only
consecutive ones are not compatible....
Of course 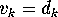 , so we see how, by choosing to view the
constraints as arrayed in a circle, Kaplansky has gotten back on the
track of the straight-forward solution. We can only admire
Kaplansky's cleverness in rediscovering the circle, and regret the
tradition of seating the ladies first that made such cleverness
necessary.
, so we see how, by choosing to view the
constraints as arrayed in a circle, Kaplansky has gotten back on the
track of the straight-forward solution. We can only admire
Kaplansky's cleverness in rediscovering the circle, and regret the
tradition of seating the ladies first that made such cleverness
necessary.
Next: Conclusion
Up: Non-sexist solution of the
Previous: Solution to the
Peter Doyle
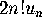 , where
, where 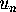 is the number of
permutations of
is the number of
permutations of 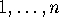 which do not satisfy any of the following
which do not satisfy any of the following
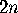 conditions: 1 is 1st or 2nd, 2 is 2nd or 3rd,...,
conditions: 1 is 1st or 2nd, 2 is 2nd or 3rd,...,  is
is  th or 1st.
Now let us select a subset of
th or 1st.
Now let us select a subset of 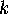 conditions from the above
conditions from the above 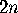 and
inquire how many permutations of
and
inquire how many permutations of 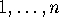 there are which satisfy
all
there are which satisfy
all 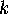 ; the answer is
; the answer is 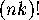 or 0 according as the
or 0 according as the 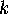 conditions are
compatible or not. If we further denote by
conditions are
compatible or not. If we further denote by 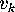 the number of ways of
selecting
the number of ways of
selecting 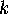 compatible conditions from the
compatible conditions from the 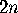 , we have, by the
familiar argument of inclusion and exclusion,
, we have, by the
familiar argument of inclusion and exclusion,  .
It remains to evaluate
.
It remains to evaluate 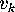 , for which purpose we note that the
, for which purpose we note that the 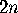 conditions, when arrayed in a circle, have the property that only
consecutive ones are not compatible....
conditions, when arrayed in a circle, have the property that only
consecutive ones are not compatible....
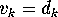 , so we see how, by choosing to view the
constraints as arrayed in a circle, Kaplansky has gotten back on the
track of the straight-forward solution. We can only admire
Kaplansky's cleverness in rediscovering the circle, and regret the
tradition of seating the ladies first that made such cleverness
necessary.
, so we see how, by choosing to view the
constraints as arrayed in a circle, Kaplansky has gotten back on the
track of the straight-forward solution. We can only admire
Kaplansky's cleverness in rediscovering the circle, and regret the
tradition of seating the ladies first that made such cleverness
necessary.