Exercises
Next: References
Up: Non-sexist solution of the
Previous: Conclusion
We list here, in the guise of exercises, some questions that you may
want to
explore with the help of the references listed.
-
Show how to ``derive'' the formula for
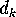 simply by writing down
the answer, without using recurrence relations or generating functions or what
have you.
(Hint: Try this first for the formula for
simply by writing down
the answer, without using recurrence relations or generating functions or what
have you.
(Hint: Try this first for the formula for 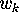 .)
.)
-
Was it really sexism that made the ménage problem appear
difficult?
(See Kaplansky and Riordan
[6], and the references listed there.)
-
Solve the analog of the ménage problem for the situation depicted
in Figure 2.
(No one is allowed to sit next to or across from his or her partner.)

Figure: Real-world ménage problem.
-
Formulate the analog of the ménage problem for an arbitrary
graph
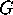 , and
show that it leads to a domino problem on
, and
show that it leads to a domino problem on 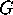 . Show that by seating
the ladies or gentlemen first, and following Kaplansky's lead, we arrive at a
problem of how to place rooks on a chessboard.
(See Riordan
[9], Ch. 7.)
Show that the domino problem and the rook problem are equivalent.
Look into the
relationship of the
domino problem to the Ising model of statistical mechanics. (See
Fisher
[3],
Kasteleyn
[7].)
. Show that by seating
the ladies or gentlemen first, and following Kaplansky's lead, we arrive at a
problem of how to place rooks on a chessboard.
(See Riordan
[9], Ch. 7.)
Show that the domino problem and the rook problem are equivalent.
Look into the
relationship of the
domino problem to the Ising model of statistical mechanics. (See
Fisher
[3],
Kasteleyn
[7].)
-
What problem was Tait
[12]
really interested in? Did Gilbert
[4]
solve it?
Show that Gilbert could have used a simple Möbius inversion
argument instead of
Pólya's theorem. What kinds of problems require the full force of
Pólya's theorem?
-
What does it mean to ``solve'' a combinatorial problem like the
ménage problem? Is a closed-form solution better than a recurrence? What if
what we really want is to generate configurations, rather than just count them?
(See Wilf
[14].)
-
Why did Tait not pursue the ménage problem? What do knots have
to do with atomic spectra? What was it like to live in Nebraska in the 1880's?
(See Conway
[2].)
-
The relaxed ménage problem can be further generalized as
follows: Given two graphs
 and
and  with the same number of
vertices, find the number of one-to-one mappings of the vertices of
with the same number of
vertices, find the number of one-to-one mappings of the vertices of
 onto the vertices of
onto the vertices of  such that no pair of vertices that are
adjacent in
such that no pair of vertices that are
adjacent in  get sent to vertices that are adjacent in
get sent to vertices that are adjacent in  . Show
that the dinner table problem (see Aspvall and Liang
[1], Robbins
[10])
can be phrased in these terms, and give a solution using
inclusion-exclusion. Formulate and solve an ``unrelaxed'' version of
this problem. Show that the ménage problem can be phrased in these
terms, and discuss how useful this reformulation is. Do the same for
the problem of enumerating Latin rectangles (see Ryser
[11]
).
. Show
that the dinner table problem (see Aspvall and Liang
[1], Robbins
[10])
can be phrased in these terms, and give a solution using
inclusion-exclusion. Formulate and solve an ``unrelaxed'' version of
this problem. Show that the ménage problem can be phrased in these
terms, and discuss how useful this reformulation is. Do the same for
the problem of enumerating Latin rectangles (see Ryser
[11]
).
Next: References
Up: Non-sexist solution of the
Previous: Conclusion
Peter Doyle
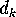 simply by writing down
the answer, without using recurrence relations or generating functions or what
have you.
(Hint: Try this first for the formula for
simply by writing down
the answer, without using recurrence relations or generating functions or what
have you.
(Hint: Try this first for the formula for 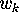 .)
.)

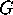 , and
show that it leads to a domino problem on
, and
show that it leads to a domino problem on 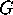 . Show that by seating
the ladies or gentlemen first, and following Kaplansky's lead, we arrive at a
problem of how to place rooks on a chessboard.
(See Riordan
[9], Ch. 7.)
Show that the domino problem and the rook problem are equivalent.
Look into the
relationship of the
domino problem to the Ising model of statistical mechanics. (See
Fisher
[3],
Kasteleyn
[7].)
. Show that by seating
the ladies or gentlemen first, and following Kaplansky's lead, we arrive at a
problem of how to place rooks on a chessboard.
(See Riordan
[9], Ch. 7.)
Show that the domino problem and the rook problem are equivalent.
Look into the
relationship of the
domino problem to the Ising model of statistical mechanics. (See
Fisher
[3],
Kasteleyn
[7].)
 and
and  with the same number of
vertices, find the number of one-to-one mappings of the vertices of
with the same number of
vertices, find the number of one-to-one mappings of the vertices of
 onto the vertices of
onto the vertices of  such that no pair of vertices that are
adjacent in
such that no pair of vertices that are
adjacent in  get sent to vertices that are adjacent in
get sent to vertices that are adjacent in  . Show
that the dinner table problem (see Aspvall and Liang
[1], Robbins
[10])
can be phrased in these terms, and give a solution using
inclusion-exclusion. Formulate and solve an ``unrelaxed'' version of
this problem. Show that the ménage problem can be phrased in these
terms, and discuss how useful this reformulation is. Do the same for
the problem of enumerating Latin rectangles (see Ryser
[11]
).
. Show
that the dinner table problem (see Aspvall and Liang
[1], Robbins
[10])
can be phrased in these terms, and give a solution using
inclusion-exclusion. Formulate and solve an ``unrelaxed'' version of
this problem. Show that the ménage problem can be phrased in these
terms, and discuss how useful this reformulation is. Do the same for
the problem of enumerating Latin rectangles (see Ryser
[11]
).