


Next: Relation to strength estimate
Up: Quasi-orthogonality on the boundary
Previous: Quasi-orthogonality on the boundary
Semiclassical estimate of off-diagonal strength of 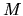
This and the next section can be skipped on first reading.
We would like an estimate of the strength of the off-diagonal part of 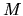 ,
which we call
,
which we call 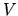 .
Writing the strength of
.
Writing the strength of 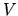 in terms of the band profile, we have
in terms of the band profile, we have
which followed from (6.9), (2.48)
and the Weyl form[35,12]
for the mean level spacing
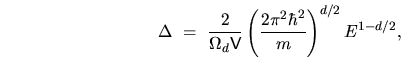 |
(6.13) |
where
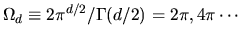 is the surface area of the unit sphere in
is the surface area of the unit sphere in 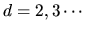 dimensions.
The `distance' from the diagonal is expressed either as a frequency
dimensions.
The `distance' from the diagonal is expressed either as a frequency
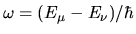 or as the wavenumber difference
or as the wavenumber difference
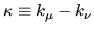 . The two are related by
. The two are related by
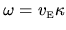 ,
where the particle speed is
,
where the particle speed is
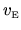 at energy
at energy 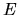 .
The band profile has been written
in a scaled form
.
The band profile has been written
in a scaled form
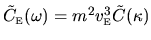 .
This scaled band profile
.
This scaled band profile
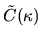 depends only on the billiard
geometry (it is independent of
depends only on the billiard
geometry (it is independent of 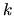 ), because the system has hard walls.
It has universal forms at both large and small
`distances' from the diagonal.
The crossover happens at typical correlation scales of the system,
given by the system size, namely at
), because the system has hard walls.
It has universal forms at both large and small
`distances' from the diagonal.
The crossover happens at typical correlation scales of the system,
given by the system size, namely at
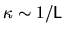 .
In this intermediate region there is non-universal system-specific
structure--e.g. see the band profile in Fig. 3.7 (graph DI).
The equivalence of classical and quantum band profiles
was demonstrated in Section 2.3.
.
In this intermediate region there is non-universal system-specific
structure--e.g. see the band profile in Fig. 3.7 (graph DI).
The equivalence of classical and quantum band profiles
was demonstrated in Section 2.3.
For
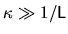 we have
we have
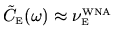 (see
Section 3.2), which upon substitution into (6.11) gives
(see
Section 3.2), which upon substitution into (6.11) gives
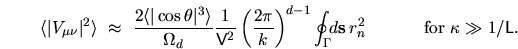 |
(6.14) |
This corresponds to a random-wave assumption for the eigenstates
(Section 3.2.1), giving no dependence on 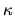 (flat band
profile).
Since we have
(flat band
profile).
Since we have
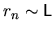 , this gives roughly
, this gives roughly
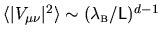 , the inverse number
of wavelength-sized patches on the boundary.
, the inverse number
of wavelength-sized patches on the boundary.
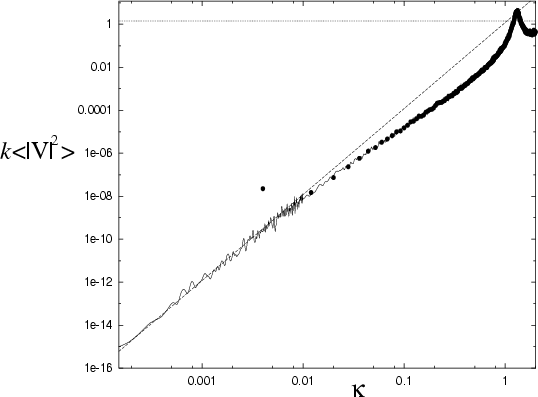
Figure 6.3:
Strength of off-diagonal elements 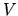 of the quasi-orthogonal matrix
of the quasi-orthogonal matrix 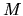 ,
for the
,
for the 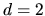 quarter stadium billiard.
The vertical axis
quarter stadium billiard.
The vertical axis
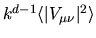 is a quantity
dependent only on the billiard system (not on
is a quantity
dependent only on the billiard system (not on 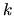 ).
The horizontal axis is the wavenumber difference
).
The horizontal axis is the wavenumber difference
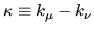 .
The solid line is the semiclassical estimate (taken from the classical
band profile). The estimation error changes at
.
The solid line is the semiclassical estimate (taken from the classical
band profile). The estimation error changes at 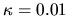 , allowing
a dynamic range of 16 orders of magnitude.
The quantum band profile (taken from the matrix of Fig. 6.2)
is shown as dots, and it becomes unreliable at the level
, allowing
a dynamic range of 16 orders of magnitude.
The quantum band profile (taken from the matrix of Fig. 6.2)
is shown as dots, and it becomes unreliable at the level 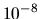 ,
for this choice of
,
for this choice of 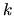 .
The dashed line is the fit to (6.15); the dotted is the random wave
result (6.14). The two lines meet at a
.
The dashed line is the fit to (6.15); the dotted is the random wave
result (6.14). The two lines meet at a 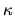 around the inverse system size
around the inverse system size
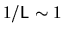 .
.
 |
Quasi-orthogonality (and the resulting success of the VS method)
is determined by very small elements close to the diagonal.
Here we have
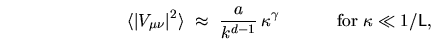 |
(6.15) |
where we seek the prefactor 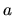 , which will depend only on the billiard shape.
The prefactor is proportional to the fluctuations intensity
, which will depend only on the billiard shape.
The prefactor is proportional to the fluctuations intensity
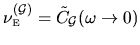 for the signal
for the signal
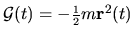 (see Section 3.3.1).
This signal has a variance of
(see Section 3.3.1).
This signal has a variance of
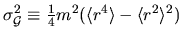 about its mean.
A rough estimate is
about its mean.
A rough estimate is
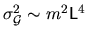 .
The intensity is the product of the variance and the correlation time:
.
The intensity is the product of the variance and the correlation time:
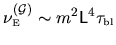 .
Therefore
.
Therefore
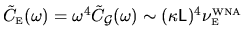 .
Thus the prefactor is
.
Thus the prefactor is
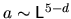 .
The accuracy is limited because we lack knowledge of the correlation time of
the signal
.
The accuracy is limited because we lack knowledge of the correlation time of
the signal
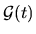 .
In the 2D quarter stadium billiard (of size
.
In the 2D quarter stadium billiard (of size
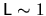 , see Fig. 2.6)
the prefactor is measured to be
, see Fig. 2.6)
the prefactor is measured to be 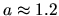 ,
remarkably close to unity (see Fig. 6.3).
It seems that convergence to the fourth-power law is very slow in this
system, not becoming accurate until
,
remarkably close to unity (see Fig. 6.3).
It seems that convergence to the fourth-power law is very slow in this
system, not becoming accurate until 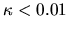 .
This is probably due to long tails in the time correlations
(Section 3.4) which makes
.
This is probably due to long tails in the time correlations
(Section 3.4) which makes
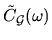 close to singular at
close to singular at 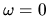 .
More study is needed of this convergence to the asymptotic form.
In systems without these non-generic effects, we expect more rapid convergence
to the fourth-power law (for instance Fig. 3.6),
and therefore better quasi-orthogonality.
.
More study is needed of this convergence to the asymptotic form.
In systems without these non-generic effects, we expect more rapid convergence
to the fourth-power law (for instance Fig. 3.6),
and therefore better quasi-orthogonality.
Both the above estimates are for
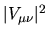 averaged over
an energy range as in Section 2.2.2, with
averaged over
an energy range as in Section 2.2.2, with 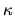 held fixed.
The Random Matrix Theory assumption is that the elements
held fixed.
The Random Matrix Theory assumption is that the elements 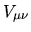 are
independent normally-distributed random quantities.
However, deviations from strong chaos (due to periodic orbits and scars; see
Section 2.3.3) will affect the distribution and correlation
of the elements.
are
independent normally-distributed random quantities.
However, deviations from strong chaos (due to periodic orbits and scars; see
Section 2.3.3) will affect the distribution and correlation
of the elements.
Thus we have estimated a wave overlap quantity semiclassically.
In both the above expressions all the dependence on `particle
quantities' (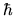 ,
, 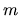 ,
,
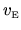 )
has cancelled, which is necessary since the
particle picture is merely a construction allowing semiclassical estimates.
(For instance in an acoustic Helmholtz application the particle model is
completely fictitious).
Rather, everything is in terms of lengths, as expected since the matrix elements
of
)
has cancelled, which is necessary since the
particle picture is merely a construction allowing semiclassical estimates.
(For instance in an acoustic Helmholtz application the particle model is
completely fictitious).
Rather, everything is in terms of lengths, as expected since the matrix elements
of 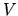 arise purely from wave considerations.
arise purely from wave considerations.



Next: Relation to strength estimate
Up: Quasi-orthogonality on the boundary
Previous: Quasi-orthogonality on the boundary
Alex Barnett
2001-10-03
![]() ,
which we call
,
which we call ![]() .
Writing the strength of
.
Writing the strength of ![]() in terms of the band profile, we have
in terms of the band profile, we have
![]() we have
we have
![]() (see
Section 3.2), which upon substitution into (6.11) gives
(see
Section 3.2), which upon substitution into (6.11) gives

![]() averaged over
an energy range as in Section 2.2.2, with
averaged over
an energy range as in Section 2.2.2, with ![]() held fixed.
The Random Matrix Theory assumption is that the elements
held fixed.
The Random Matrix Theory assumption is that the elements ![]() are
independent normally-distributed random quantities.
However, deviations from strong chaos (due to periodic orbits and scars; see
Section 2.3.3) will affect the distribution and correlation
of the elements.
are
independent normally-distributed random quantities.
However, deviations from strong chaos (due to periodic orbits and scars; see
Section 2.3.3) will affect the distribution and correlation
of the elements.
![]() ,
, ![]() ,
,
![]() )
has cancelled, which is necessary since the
particle picture is merely a construction allowing semiclassical estimates.
(For instance in an acoustic Helmholtz application the particle model is
completely fictitious).
Rather, everything is in terms of lengths, as expected since the matrix elements
of
)
has cancelled, which is necessary since the
particle picture is merely a construction allowing semiclassical estimates.
(For instance in an acoustic Helmholtz application the particle model is
completely fictitious).
Rather, everything is in terms of lengths, as expected since the matrix elements
of ![]() arise purely from wave considerations.
arise purely from wave considerations.