Rational Maps with Symmetry.

To compute extensions, one must use rational maps with icosahedral symmetry. In this section will construct all rational maps with given symmetries, using invariant polynomials. We then give a conceptual proof of the existence of the map claimed in Lemma 4.5, and also obtain concrete formulas for use in the solution of the quintic.

Let be a finite group of Möbius transformations. How can we construct rational maps such that ?

Here are three ways to construct such f.

I. Projectively Natural Newton's Method. Ordinary Newton's method applied to a rational function p(z) can be thought of as the map which sends z to , where A(z) is the unique automorphism of whose 1-jet matches that of p at z. If one replaces A(z) by the unique Möbius\ transformation of whose 2-jet agrees with that of p, then the resulting iteration,

is `projectively natural', in the sense that for any Möbius transformation . Thus contains whenever p(z) is -invariant (and such p are easily constructed).

II. Geometric Constructions. Consider, for example, the case of the icosahedral group. Tile the Riemann sphere by congruent spherical pentagons, in the configuration of a regular dodecahedron (the dual to the icosahedron). Construct a conformal map from each face of the dodecahedron to the complement of its opposite face, taking vertices to opposite vertices. (See Figure 4.) The maps piece together across the boundaries of the faces, yielding a degree 11 rational map f(z) with fixed points at the face centers and critical points at each vertex. Since the notions of `opposite face' and `opposite vertex' are intrinsic, the map commutes with the icosahedral group.

  
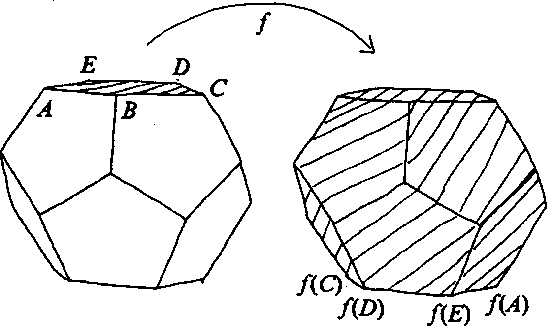
Figure 4: Geometric construction of a rational map.

This construction has many variants. For example, it can be applied to the 20 faces of the icosahedral triangulation, giving a rational map of degree 19, or to the tiling by 30 rhombuses, giving a map of degree 29. (This last tiling, which may be unfamiliar, is by Dirichlet fundamental domains for the 30 edge-midpoints of the dodecahedron. Each rhombus marks the territory which is closer (in the spherical metric) to one of the 30 points than to any other.)

III. Algebraic Constructions. Our final method suffices to produce all rational maps with given symmetries. It will make clear, for example, that the three maps just constructed, together with the identity, are the only maps of degree < 31 with icosahedral symmetry.

Let E be a 2-dimensional complex vector space.

A point p on corresponds to a line in E hence to a linear functional with this line as its kernel. A collection of n points corresponds to a homogeneous polynomial of degree n, vanishing along the lines corresponding to the n points. Like the linear map corresponding to a single point, this polynomial is only well-defined up to multiplication by an element of .

A rational map corresponds to a homogeneous polynomial map . X can be obtained by homogenizing the numerator and denominator of f.

Since the tangent space to any point of E is canonically isomorphic to E, X can also be considered as a homogeneous vector field on E.

Now let be a finite group, its pre-image in the group of linear maps of determinant 1. A vector field X on E is invariant if there exists a character such that for all in . X is absolutely invariant if the character is trivial.

The action of on vector fields goes over to the action of by conjugation on rational maps, establishing:

P 5.1. contains if and only if the corresponding vector field X(v) is -invariant.

Remarks.

\

1. The possibility of a character arises because f(z) determines X(v) only up to scale.

2. For a 2-dimensional vector space, and are canonically isomorphic; thus a rational map also determines a homogeneous 1-form , unique up to scale.

3. A rational map of degree n determines a 1-form which is homogeneous of degree n+1; the converse is true unless for some homogeneous polynomial g and 1-form with . In this case the numerator and denominator of the corresponding rational function are not relatively prime.

4. A homogeneous polynomial h(v) determines an exact 1-form dh(v); thus a configuration of n+1 points on naturally determines a rational map of degree n.

Let x and y be a basis for . The 1-form

is an absolute SL(E) invariant, as well as a primitive for the invariant volume form . The rational map corresponding to is the identity ( annihilates the line through v).

T 5.2. A homogeneous 1-form is invariant if and only if

where f and g are invariant homogeneous polynomials with the same character and .

Proof. Suppose is invariant. The exterior derivative , where h(v) is a homogeneous polynomial. Since is an absolute invariant of , h(v) is invariant with the same character as . Setting , it is easy to check that and hence is closed. Integrating this closed form along lines from the origin yields its unique homogeneous primitive g (v); by uniqueness, g(v) is invariant with the same character as .

The converse is clear; the condition on degrees assures that the sum is homogeneous.

The construction of invariant rational maps is thus reduced to the problem of invariant homogeneous polynomials. The latter correspond simply to finite sets of points on , invariant under , and are easily described.

Example: The Icosahedral Group.

\

Identify the Riemann sphere with a round sphere in so that 0 and are poles and |z| = 1 is the equator. Inscribe a regular icosahedron in the sphere normalized so one vertex is at 0 and an adjacent vertex lies on the positive real axis (in ). Then the isometries of the icosahedron act on by a group isomorphic to . This particular normalization agrees with the conventions of [8] and [2].

Since the abelianization of the binary icosahedral group is zero, every invariant is an absolute invariant.

We identify with , and choose a basis for such that the coordinate z on is equal to x/y.

There are three special orbits for the action of : the 12 vertices, 20 face-centers and 30 edge-midpoints of the icosahedron. The corresponding invariant polynomials, derived in [8], are:

Every other orbit has cardinality 60, and corresponds to a linear combination of the degree 60 invariants , and (which satisfy the relation ). Thus every homogeneous polynomial invariant under the binary icosahedral group is a polynomial in f, H and T.

P 5.3. There are exactly four rational maps of degree < 31 which commute with the icosahedral group. Then these four maps, of degree 1, 11, 19, and 29 respectively are:

Proof. An invariant rational map of degree < 31 corresponds to an invariant 1-form of degree < 32. The only invariant homogeneous polynomials of degree < 32 are f, H and T. Since no two of their degrees differ by 2, we conclude from Theorem 5.2 that the invariant 1-forms of degree < 32 are proportional to either or dg (v), where g is equal to f, H or T. The rational maps corresponding are the identity, while those corresponding to df, dH and dT are the other three maps computed above.

Remark. One may glean from the footnote on page 345 of [9] that these maps were known as well to Klein.

Proof of lemma 4.5 (Existence of an Icosahedral Algorithm). Consider the map . We claim the critical points of reside at the 20 vertices of a spherical regular dodecahedron, and are each mapped to their antipodal vertices under one iteration. This is clear from the geometric construction of (method II above).

It can also be verified by counting. has 20 critical points, which must be a union of orbits of ; the only such orbit corresponds to the vertices of a dodecahedron. Each vertex has an stabilizer in ; since commutes with the group action, the image vertex is fixed by the same subgroup. A simple critical point which is fixed cannot commute with the action; hence the corresponding critical value must be the antipodal vertex.

Thus is critically finite, and almost every point is attracted to periodic cycles of order two lying at pairs of antipodal vertices. The map satisfies the hypotheses of the Lemma.

Remarks.

\

1. There is a one-parameter family of invariant rational maps of degree 31, which will be used to construct in in our explicit solution of the quintic.

2. Let p(z) be a polynomial of degree d. Consider radically modified Newton's method:

is the unique rational map of degree (d-1) with fixed points at the roots of p and derivative (1-d) at each fixed point. When d = 2, is a Möbius transformation of order two fixing the roots of p; for d > 2 the roots are repelling. (Thus is not suggested as a method to find roots of p.)

coincides with the rational map naturally associated to the roots of p by exterior derivative of the corresponding homogeneous polynomial, as discussed above. This observation will simplify the description of our explicit iterative scheme for the quintic: we need only specify p.