In this appendix we will describe a concrete algorithm for solving the general quintic equation. This algorithm is based on Klein's theory of the connection between the general quintic and the icosahedral equation, described in his famous lectures on the icosahedron [8]. See also [4] (from which we take the illustration below), and [2]. We begin by reviewing this theory.
Associated with the icosahedron
(normalized as in §5)
is a tiling of the
Riemann sphere by 120 spherical triangles,
60 black and 60 white (Figure 5).
This configuration is invariant under the icosahedral group,
represented as a group 
of Möbius transformations.
Each triangle has angles 
corresponding to the 30 edge midpoints, 20 face centers, and 12 vertices of
the icosahedron.
We will refer to these special points as 2-, 3-, and 5-vertices.
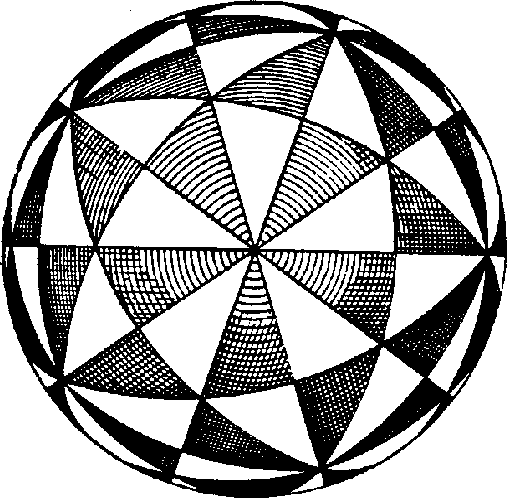
Figure 5: The icosahedral tiling.
Map each white triangle conformally to the upper half-plane,
and map each black triangle conformally to the lower half-plane,
so that the 3-, 5-, and 2-vertices map to 
.
These 120 separate mappings piece together
to give a rational function of degree 60,
the icosahedral function.
This function, denoted by 
, is
right-invariant under the
icosahedral group :
it gives the quotient map 
.
To write down the icosahedral function explicitly,
recall that every homogeneous polynomial invariant under the
binary icosahedral group 
is a polynomial in
, 
, and 
, where
The polynomials , , and
vanish at the 5-, 3-, and 2-vertices respectively.
They satisfy the identity
The icosahedral function 
is
To check this, note that the top and bottom are homogeneous
of degree 60 (so the ratio is a rational function of
),
the zeros and poles occur at the 3- and 2- vertices, and
by the identity
the 5-vertices of the icosahedron are mapped to 1.
The equation
is called the icosahedral equation.
Solving the icosahedral equation amounts to finding one of the 60
points that map to Z under the icosahedral function.
Given one such point,
the 59 others can be found by determining the images of the first
under the group .
Please note that our normalization of the icosahedral function differs from the normalizations of [8] and [2]:
In this section we give a brief account of the classical reduction of the general quintic equation
to the icosahedral equation, following [8]. As Klein emphasized, this reduction is best understood geometrically.
The first step in the reduction dates back to 1683, when Tschirnhaus showed that by making a substitution of the form
the general quintic can be reduced to
a quintic for which 
.
Here a and b are determined by solving an
auxiliary quadratic equation.
Such a quintic is called a principal quintic.
Equivalently, a principal quintic is one normalized
so its roots satisfy 
.
These homogeneous equations determine a quadric surface in
the projective space of roots.
Viewed geometrically, the Tschirnhaus transformation
moves an ordered set of roots to one of the two
points of intersection of this quadric with the line
determined by allowing a and b to vary.
Which point depends on the
choice of auxiliary root.
The symmetric group 
acts
on the quadric by permuting the roots.
An odd permutation interchanges the two rulings
of the quadric by lines;
adjoining with square-root of the discriminant
reduces the action to the alternating group 
,
which preserves the rulings.
The space of lines in a given ruling is isomorphic to
the Riemann sphere 
, and in appropriate
coordinates the action of
(on the space of lines) is none other than the
icosahedral action.
From the original principal quintic and the square-root
of its discriminant, we may determine a point Z on
the quotient such that a solution to
corresponds to a line containing the point
for some ordering
of the roots. Then the roots themselves can be
found by elimination.
Perhaps the most intriguing part of this whole story is the square root
used in the Tschirnhaus transformation to obtain a
principal quintic.
This square root is an accessory irrationality,
as it does not diminish the Galois group of the equation,
and as such is not expressible in terms of the roots of the equation.
Rather, its function (as pointed out in [15])
is to eliminate the cohomological obstruction described in
.
The culmination of Klein's lectures on the icosahedron
is the result,
which Klein calls Kronecker's theorem,
that without the introduction of such an accessory irrationality
the general quintic equation cannot be reduced to a resolvent equation
that depends--like the icosahedral equation--on a single parameter.
While this result was stated by Kronecker,
the first correct proof was given by Klein.
Apparently, Kronecker felt that accessory irrationalities
were `algebraically worthless',
and proposed what he called the `Abelian Postulate',
requiring that such accessory irrationalities be avoided at all costs.
According to this view,
the reduction of the quintic to the icosahedral equation is inadmissible.
Arguing against this point of view,
Klein (on page 504 of [9])
writes:
Soll man, wo sich neue Erscheinungen (oder hier die Leistungsfähigkeit der akzessorischen Irrationalitäten) darbieten, zugunsten einer einmal gefassten systematischen Ideenbildung die Weiterentwicklung abschneiden, oder vielmehr das systematische Denken als zu eng zurückschieben und den neuen Problemen unbefangen nachgehen? Soll man Dogmatiker sein oder wie ein Naturforscher bemüht sein, aus den Dingen selbst immer neu zu lernen?(When new phenomena appear, like the efficacy of the accessory irrationality, should we halt our investigations because the facts fail to agree with our preconceived notions, or should we cast aside those preconceived notions as being too narrow, and pursue the new problems wherever they lead? Should we be dogmatists, or should we--like experimental scientists--try always to learn from the facts themselves?)
The algorithm we are going to develop to solve the general quintic proceeds by computing a root, not of the icosahedral equation itself, but of a certain quintic resolvent.
Algebraically, the icosahedral equation determines an
extension of function fields k'/k,
where
and 
.
A quintic resolvent is the irreducible polynomial
satisfied by an element of k' of degree 5 over k.
In this section, we will derive formulas for the tetrahedral and Brioschi resolvents, again following [8]. The Brioschi resolvent is a one parameter family of quintics, to which the general quintic may be reduced; it is this equation we will actually solve. The tetrahedral resolvent is used to determine a root from the limit point of an iteration.
Figure 6: A cube inscribed in the icosahedron.
The root of a quintic resolvent is stabilized by
an 
subgroup of .
There are five such tetrahedral subgroups
in , all conjugate.
One tetrahedral subgroup, which we denote 
, is distinguished
because it leads to a resolvent defined over 
.
can be described geometrically as follows.
There are five cubes whose vertices lie on the vertices
of a regular dodecahedron. Of these, exactly one is
symmetric with respect to reflection through the real axis;
the intersection of its symmetry group with is
.
The vertices of this cube, and the one-skeleton of its
dual octahedral (which includes the real axis),
appear in Figure 6.
permutes the 12 pentagons that correspond to faces of the dodecahedron,
and any one of them is a fundamental domain for .
preserves the 6 vertices of the dual octahedron,
and the 4 vertices of each tetrahedron inscribed in the cube;
the stabilizers of all other points are trivial.
Note that only half of the symmetries of the cube (and octahedron)
are symmetries of the icosahedron; otherwise
would have a subgroup of order 24.
Besides the special orbits of ,
we need to pay attention to two orbits of order 12:
the face centers of the dodecahedron,
i.e., the 5-vertices,
and the 20 - 8 = 12 complementary 3-vertices--the
vertices of the icosahedron which do not lie on the cube.
There is a tetrahedral function 
, analogous to the
icosahedral function ,
which gives
the quotient map 
.
By composing with a Möbius transformation,
this function can be normalized to take specified values
on any three orbits of .
We choose the normalization so that the 5-vertices
map to 
,
the vertices of the octahedron map to 0,
and the complementary 3-vertices map to 3.
To write down a formula for ,
we call forth some of the invariant forms for the
binary tetrahedral group 
.
Fortunately,
all the forms that we need to work with are
absolute invariants (no character of appears).
Those we use,
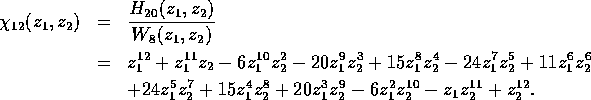
vanish at the vertices of the octahedron, the cube, and the complementary 3-vertices respectively.
Any invariant form of degree 12 is a linear combination of the forms
, 
, and ,
which satisfy the identity
Thus
since this expression has zeros and poles in the right places, and the identity
shows the complementary 3-vertices are mapped to 3 as desired.
Under , the 60 roots of the icosahedral equation
map in groups of 12 to 5 distinct points. In terms of a single root z, these 5 images are
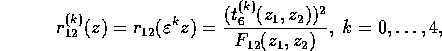
where
and 
is a fifth root of unity.
(The rotation 
is an element of ).
The quintic resolvent for 
turns out to be
We will call this equation the tetrahedral resolvent.
Algebraically, the functions 
are just the roots
of the tetrahedral resolvent in the function field setting.
This equation can be derived entirely geometrically,
without recourse to the explicit formulas for .
(See pages 100-102 of [8].)
The related function 
given by
satisfies the Brioschi resolvent
where C = (1-Z)/1728; the roots of this equation are:
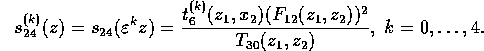
Any principal quintic can be reduced to the Brioschi resolvent for some particular choice of C, determined rationally in terms of the original coefficients and the square-root of the discriminant. This reduction appears in detail in [2].
We are now ready to concoct a generally convergent
algorithm for the icosahedral field extension
k'/k.
The ingredients for such an algorithm are given
in Theorem 4.1; note that the Galois group,
, is tautologically identified with
a group of Möbius transformations.
The algorithm itself is specified by
,
and
,
depending on a root z of the icosahedral equation,
such that
for all 
in .
by (a) and (b) 
and so T
only depends upon 
.
To make the formulas as simple as possible, we will choose
, the unique lowest degree rational map with
icosahedral symmetry and a non-trivial attractor (see §5).
(The attractor of 
is periodic of order 2, so we
will actually iterate 
.)
As for 
, note that for each fixed w the map
is a rational map with icosahedral symmetry.
As mentioned in Remark 1 of §5, there is a one-parameter
family of symmetric maps of degree 31 (and none of smaller degree);
this provides the simplest candidate for 
.
There are three points at which this family degenerates to
maps of lower degree 
, , and 
; we arrange
that these degenerations occur at 
, 0 and 1.
To derive a formula for 
in terms of Z, we begin
by expressing in homogeneous coordinates
then
To check this formula, we just need to verify that it
degenerates as described above.
Clearly this is true for w=0 and .
For w=1 the rational map we get is
which agrees with by virtue of the identity
To get the formula for 
, we note
is canonically associated to the
12 vertices of the icosahedron, so T is
canonically associated to their images under 
.
By remark 2 at the end of §5, all we must do
to specify is to give a polynomial g(Z,w)
having these 12 points as its roots.
This leads us to look at the form
,
where 
is the homogeneous version of given above.
The form G is homogeneous of degree 
in
and of degree 12 in 
.
This polynomial is symmetric under the action of on .
Because the ring of -symmetric forms is generated by
and ,
and because 
,
it follows on numerological grounds that G is divisible by ,
and that the quotient 
can be written
as a homogeneous polynomial of degree 6 in 
and of degree 12 in .
This polynomial can be found by solving a large system of linear equations.
Dividing the resulting expression
for through by 
and using the fact that 
,
we get
where g is a polynomial with integer coefficients, exhibited at the end of this Appendix. We found the coefficients of g by solving the relevant system of equations with the aid of a computer.
The map is now given by
where g' denotes the derivative of g with respect to w.
Under the iteration
almost every starting guess is attracted to a cycle
of period 2
consisting of one of the 10 pairs of antipodal 3-vertices.
If instead iterating we iterate ,
then almost every starting guess
is attracted to a single one of the 20 3-vertices.
The map is just
transported to new coordinates by .
For almost every Z, almost every starting guess converges under
iteration of 
to
where e is one of the 20 3-vertices of the icosahedron in its standard location.
Of course to be able to write
we have to select some particular root z of the icosahedral equation, for we could equally well write
Turning this around,
we see that if we choose some particular 3-vertex 
,
there will be exactly three choices for the root z
for which
These three choices differ from one another by the action
of the stabilizer 
of the 3-vertex .
Therefore from 
we can
determine the values
of two of the functions 
,
and hence two roots 
, 
of the Brioschi resolvent.
These two values
correspond to the two tetrahedral ( ) subgroups of
that contain the stabilizer of .
As ranges over the 20 attractors of ,
the pair 
ranges over the 20 ordered pairs of
roots of the resolvent.
In particular,
going from to the `antipodal point' 
,
we get the same pair of roots in the opposite order.
To determine and explicitly in terms of ,
we introduce the function
While expressed in terms of z,
this function really only depends on Z,
because the action of permutes the two sets of
factors in the same way.
The idea behind 
is that
the first factor
acts as a `selector function' for the second:
Recall that the value of function
is 3 at the complementary 3-vertices;
at the vertices of the tetrahedron and the dual tetrahedron its
values are
which are the other two roots of
Thus the factor 
vanishes for three values of k and takes on the values
for the remaining two values of k. Consequently
where 
are two roots of the Brioschi resolvent.
Replacing with the `antipodal' fixed point
exchanges the roles of and ,
so we have
Thus we get a pair of linear equations
from which we can determine and .
All that remains is to express in terms of Z and w.
Let 
be defined analogously to 
.
Then
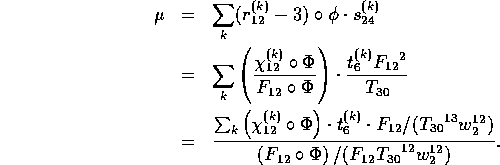
The denominator here is our old friend g(Z,w). The numerator can be expressed as a polynomial in Z and w, by the same technique used to determine g. We find
where h(Z,w) is a polynomial with integer coefficients, exhibited below.
To solve the Brioschi resolvent
we proceed in five steps.
where g(Z,w) is the polynomial in Z and w given below, and g' denotes the derivative of g with respect to w.
on a random starting guess until it converges.
Call the limit point , and set 
. 
for i = 1,2, where h is the polynomial in Z and w given below.
for i = 1,2. These are two roots of the Brioschi resolvent.
The key ingredients g(Z,w) and h(Z,w) are given by:
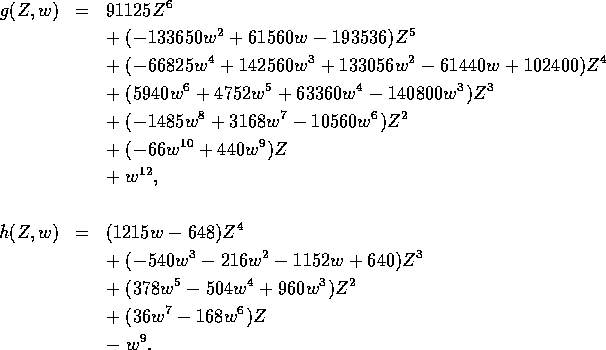
Remarks.
1. A quintic with real coefficients always has at least one real root. Curiously, when applied to a real quintic with real initial guess for step 2, our method always returns a pair of conjugate roots.
2. To find the remaining roots of the quintic, we can apply del Ferro's formula or Example 3 of section 3 to solve the quotient cubic. We could also construct a single iteration that would find all five roots at once, but the formulas might be rather more complicated.
3. Remarkably, one can also derive the formulas for g and h
by hand, without even knowing
the basic invariants , and
of the icosahedral group.
This alternate approach exploits
the large number of coefficients that vanish,
and is based on a study of degenerations
of g and h and at Z = 0, 1
and .