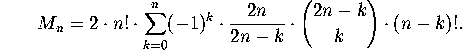Solution to the ménage problem
Next: Comparison with Kaplansky's
Up: Non-sexist solution of the
Previous: Solution to the
For the ménage problem, we proceed just as before, only now we
restrict the set 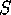 of seatings to those where men and women
alternate. The number of these seatings is
of seatings to those where men and women
alternate. The number of these seatings is 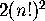 : two ways to
choose which seats are for men and which for women;
: two ways to
choose which seats are for men and which for women; 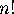 ways to
seat the men in the men's seats;
ways to
seat the men in the men's seats; 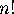 ways to seat the women in the
women's seats. Just as before, we have
ways to seat the women in the
women's seats. Just as before, we have
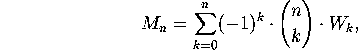
where 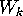 denotes the number of alternating seatings under which a
specified set of
denotes the number of alternating seatings under which a
specified set of 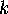 couples all end up sitting together. This time we
have
couples all end up sitting together. This time we
have
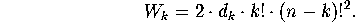
(Decide which are men's seats and which women's, where the 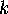 couples go, which couple goes where, and where the
couples go, which couple goes where, and where the 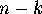 men and
men and 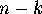 women go.) Plugging in for
women go.) Plugging in for 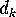 yields
yields
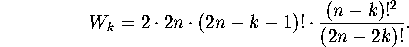
Plugging this expression for 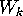 into the formula for
into the formula for 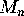 above, we
get
above, we
get
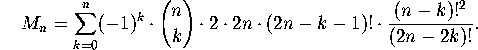
By symmetry, we know that 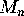 must be divisible by
must be divisible by 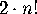 . Pulling
this factor out
in front, we can write
. Pulling
this factor out
in front, we can write
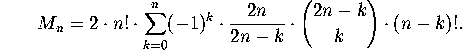
The first few values of 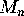 are shown in Table 2.
are shown in Table 2.
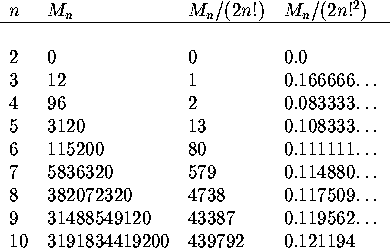
Table: Ménage numbers
Next: Comparison with Kaplansky's
Up: Non-sexist solution of the
Previous: Solution to the
Peter Doyle
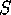 of seatings to those where men and women
alternate. The number of these seatings is
of seatings to those where men and women
alternate. The number of these seatings is 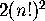 : two ways to
choose which seats are for men and which for women;
: two ways to
choose which seats are for men and which for women; 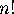 ways to
seat the men in the men's seats;
ways to
seat the men in the men's seats; 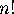 ways to seat the women in the
women's seats. Just as before, we have
ways to seat the women in the
women's seats. Just as before, we have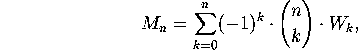
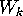 denotes the number of alternating seatings under which a
specified set of
denotes the number of alternating seatings under which a
specified set of 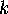 couples all end up sitting together. This time we
have
couples all end up sitting together. This time we
have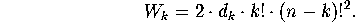
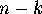 men and
men and 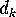 yields
yields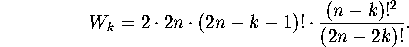
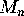 above, we
get
above, we
get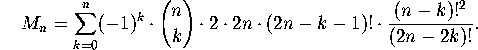
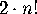 . Pulling
this factor out
in front, we can write
. Pulling
this factor out
in front, we can write