Resources Math 3 Course Home Page Math 3 Course Syllabus Practice Exams Textbook Home Page Post a Comment

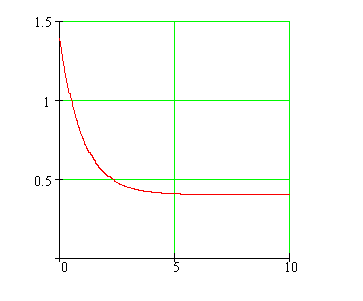
Contents In this lecture we continue with the discussion of separable differential equations. We also consider exponential growth and decay, important models in real-world applications. Quick Question Is the town population depicted in the following graph, growing, decreasing, or staying the same over the last ten years? Answer Outline Outlines for Exponential Growth and Decay Separable Differential Equations Textbook Exponential Growth and Decay Separable Differential Equations Today's Homework Log into WebWorK Quiz Exponential Growth and Decay Quiz Separable Differential Equations Quiz Examples We have a 100-gallon tank filled with water. Saltwater is being pumped into the tank through two pipes. Write an equation which states how the amount of salt S is changing with respect to time, and use the differential equation from part 1 to write a function that states how much salt is present in the tank at a given time t. A cup of coffee is initially 170 degrees Fahrenheit and is left in a room with ambient temperature 70 degrees Fahrenheit. Suppose that when the coffee is first placed in the room, it is cooling at a rate of 20 degrees per minute. Assuming Newton's law of cooling applies, how long does it take for the coffee to cool to 110 degrees? The population of fish in a pond is modeled by the differential equation dP/dt = 480 − 4P, where time t is measured in years. Towards what number does the population of fish tend? If there are initially 10 fish in the pond, how long does it take for the number of fish to reach 90% of the eventual population? Solve the differential equation dy/dx = xex2 − ln(y2) Solve the differential equation dy/dx = (x2y − 4y)/(x + 2) Solve the differential equation x dy/dx = 2(y − 4) Applets Calculator: Values of Elementary Functions Videos Radioactive decay in Earth Science determines approximate age of rocks (1) Radioactive decay in Earth Science determines approximate age of rocks (2) Separation of variables dP/dt = kP Solving the basic population growth differential equation A Population of bacteria doubles every 2.5 hours. What equation governs its growth? "The Chafing Dish" Solve the differential equation: dy/dx = (2x2 + 3x)/(y + 1)

Lecture 17 | Index | Lecture 19