Resources Math 3 Course Home Page Math 3 Course Syllabus Practice Exams Textbook Home Page Post a Comment

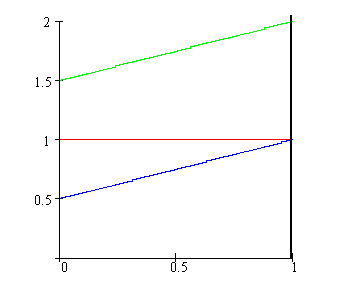
Contents In this lecture we define the definite integral and develop some of its immediate properties. Quick Question What is the total area under the sum of the two functions f(x) = 1 and g(x) = 1/2 + x/2? Answer Outline Outlines for The Definite Integral Properties of the Definite Integral Textbook The Definite Integral Properties of the Definite Integral Today's Homework Log into WebWorK Quiz The Definite Integral Quiz Properties of the Definite Integral Quiz Examples Write the following sum in sigma notation: 5/n + 50/n + 375/n + ... + (n − 1) 5(n − 1)/n. Consider the function f(x) defined to be 1 if x is in the interval [0, 1] and is rational, and 0 otherwise. Is it possible to find the area between this function and the x axis? Calculate the integral from 0 to 1 of x using the limits of Riemann sums. Evaluate the integral from −3 to 6 of |x|. Write a summation as a definite integral. Evaluate the integral from 0 to 2π of sin(x) + 5x. Applets Riemann Sums Mean Value Theorem for Integrals Videos 3 + 5 + 7 + 9 + 11 = summation from i = 0 to 4 of (3 + 2i) – 1/2 + 2/4 – 3/8 + 4/16 – 5/32 + ... + – 17/(217) Approximate area under a curve by adding areas of rectangles What integral equals the limit as n approaches ∞ of the summation from i = 0 to n of (1 + (2i/n)2) · 2/n ? Estimate area under f(x) = x2 from x = 0 to x = 2, using 5 rectangles What is the value of the integral from –3 to 0 of √(9 – x2)? Simplify the integral from –a to a of sin(2x) + x.

Lecture 21 | Index | Lecture 23