Resources Math 3 Course Home Page Math 3 Course Syllabus Practice Exams Textbook Home Page Post a Comment

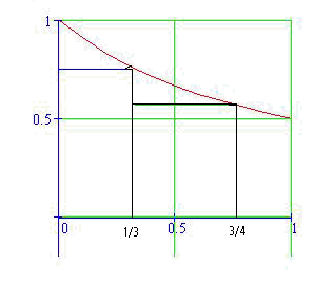
Contents In this lecture we consider a real-world application of modeling with accumulations by developing a case study on river flooding. This material is the extended application and culmination of our work in lectures 21-26. Quick Question What is the approximate area under the graph of the function 1/(1 + x) on the interval [0,1] using the two inscribed rectangles on the intervals [0,1/3] and [1/3,3/4]? (You need not simplify your answer.) Answer Outline Outline for Case Study: Flood Watch Textbook Case Study: Flood Watch Today's Homework Log into WebWorK Quiz Case Study: Flood Watch Quiz Examples Calculate the centroid of the region between the curves f(x) = x2 + 2 and g(x) = 2x + 5 for x in the interval [–1, 3]. A certain river has rainfall discharge data and rainfall recorded during and after a storm. Find the base flow of the river, the total volume of rainfall discharge, and the lag time between the rainfall event and the rainfall discharge. A flower grows at varying rates, measured at the beginning of each month and halfway through each month, according to a chart. What is the approximate height of the flower after three months? Consider a second flower that requires fertilizer to grow, and compute the lag time between the application of fertilizer and the flower's growth. Applets Flood Watch Videos Find the x coordinate of the centroid of the region bounded by y = 0, y = x2, x = 0, x = 1 Find the y coordinate of the centroid of the region bounded by y = 0, y = x2, x = 0, x = 1

Lecture 25 | Index | Lecture 27