Buying a House
Instructor notes

BHNI1

In advance of this module, the class might:

Look at real estate ads for their area. Have them bring some ads to class. Describe their dream home. The purpose of this is to get the emotional aspect on the table. Describe their parents' home (by way of contrast).

Discussion questions:

What percent of American families own a house? How many people in class own their own house? How many people's parents own their own home? What are the pros and cons of home ownership?

What do you think it would cost to fix up the house in this picture?

BHNI2

This slide introduces some words that will be explained later. It is worth pointing out that “adjustable rate” or ARM, and “points” are special features of mortgage loans that aren't used for other sorts of loans (such as credit card or car).

3/1 ARM means the interest rate is fixed for 3 years, and adjusted every year thereafter based on some index.

What's an index? It is some measure of what interest rates are doing across the country.

BHNI3

These are sample advertisements for mortgages.

So if you bought a half million dollar house, and had a roommate that you charge $1000 per month rent, you could live in this palace for only $928 per month, right?

Here it is good to talk about ad pitches. What information is left out? Especially what numerical information might be important that is left out?

How do these offers compare to the asking prices in the ads that your students found?

BHNI4

Possible discussions: What do students think is the right order to proceed? Who is involved in a house purchase?
Real estate agents (usually two of them)
Banker
Lawyer
Buyer
Seller
Who makes money on the deal?
Every one of these will make money on the sale except the buyer.
Unlike the buyer in the video, you, as the buyer, do not want to be the most ignorant person in the process.

BHNI5

Discussion:
Why is this the right order?
   There are too many houses on the market to look at all of them. You could spend days looking at places you can't buy.

How do you look at houses before you find a real estate agent?     This will be explained later, but you could see what the students think.

What do you suppose “Do the math” refers to?

Students may have already done the car module or the credit card module, and have some ideas.

BHNI6

What is “current debt obligation”? The students, with prompting, should be able to figure this out.

What is a credit report?

One example is FICO, which assigns a number between 300 (the worst) and 850 (the best). It reflects your credit record—how much credit you use and whether you have used it responsibly. If the score is too low you might not qualify for a loan at all.

What is an asset?

This refers to stuff you own that the bank thinks is important. Another house, your car, your 401k balance, your savings account, but not your dog.

What is your income?

Probably you have a job, but the bank will ask if there are other sources of income besides the job. A second job, a trust fund, rental income, etc.

BHNI7

Ratio and proportion are major topics in remedial math courses even at the college level. Here is an opportunity to compute some, discuss the use of ratios and how they work.

For example, if your housing expenses are $2,000 per month and your income is $7,000 per month, what will the housing expense ratio be? And what is the impact of choosing a property with $200 more in taxes each month?

BHNI8

It would be good to do some mental math here- 10% of various house prices, perhaps the ones on the ads the students found.

You might ask students if this all the money they think they will need to have on hand for the purchase. It isn't, of course, they will need more.

BHNI9

Be sure to print out the report that goes with the online calculator, which includes definitions of lots of terms that you will see in the financial documents the mortgage company will make you sign. Notice PMI, a special extra insurance you get to pay if your down payment is low.

Note that the calculator also allows you to put in a lower house price and see the happy result in your reduced mortgage payments.

Be sure to note that taxes vary wildly from place to place, and this is just an estimate. A particular house can come in above or below this estimate.

You may download a spreadsheet to complete all calculations in this module.

BHNI10

So the table is less accurate than the calculator, because it doesn't allow for your personal debt to be included. However, it is revealing because you can see many options at once.

Be sure students notice that the “monthly housing expense” is much higher than the mortgage payment. By now they may be able to say why: taxes, insurance.

At this point you may want to use the word “escrow”, which is a bank account the mortgage company uses to store money that you pay them every month which they will then pay out as insurance or property tax.

Notice that the web site offers other useful calculators that your students may want to use later.

BHNI11

It would be good to compare some numbers now.

How does the $150,000 house price compare with the ads that the students collected? Do they think the average price of houses they found in the ads reflects the local market? Why or why not? Real estate agents make a commission that is a fixed percentage of the selling price. How might that affect which ads they choose to place in the local paper?

How does the $60,000 of income compare to incomes in your area? How about the profession the students are preparing to enter?

How is it that relatively low income families sometimes have very valuable houses? This question might lead to a discussion of real estate as an investment that (perhaps) grows in value over time, as well as the use of the equity accumulated in the house to “trade up” to a more expensive home.

How about closing costs? Is it fair that the buyer has to cover all of these, as is usual? First of all, this is typical but could also be negotiated. Second, the seller is paying the commission to the real estate agent, which is usually more than the closing costs. The buyer's agent and the seller's agent split the commission. They in turn give some commission to the agency they represent.

BHNI12

About the MLS. This is a service real estate agents use to locate and market homes.

• The only houses listed are for sale by real estate agencies. Agencies have an agreement with each other to show their clients anything listed in the MLS. But is doesn't always work quite that way, as some agencies will resist showing you homes that are not their listing, as it reduces their commission.
• Before the internet, the MLS listing came in a big book issued at regular intervals. The real estate agent decided whether to allow you to see it, or whether to select offerings from it to show you.
• Now most listings can be found on various web sites. This is a huge advantage to the buyer if you study it carefully.

BHNI13

This particular listing was offered for $44,900 (2011). It was the least expensive of all 12 properties listed under $100,000. What do the students make of this description? Why might the house be inexpensive? Here is a chance to discuss what affects the cost of real estate.

Why might the seller only be accepting cash offers?

BHNI14

You can have students use the internet to find out something about asbestos. It brings up other issues of home ownership—you are managing a property, not just owning it.

What kinds of problems might prevent the bank from mortgaging a particular property? (No heating system in a cold climate, certain kinds of foundations, certain kinds of septic systems, etc. Do students know what a septic system is?)

BHNI15

This is for fun. Students can make up more examples. But just because it's fun doesn't make it particularly inaccurate.

About wiring: Electric stoves require 220V and almost everything else requires 110V. The V stands for “volt”, in case any of your students took physics. These should never be combined! So there are many things a homebuyer might wonder about a house. This is why there are inspections, although an inspector probably wouldn't notice such a wiring issue.

BHNI16

Why would it be important for the agent to love houses? Students can offer suggestions, but it comes down to patience.

You might ask students to estimate how long it would take them to decide what house to buy. Here is an article that estimates 4-8 months average for most people, of which 1-2 months is the closing process after choosing a house. Some, of course, take much longer.

Why is it good for you to tell the agent what you want to view, rather than waiting for the agent to make suggestions? Because you want control, among other things. However, the agent's input is very useful because they may have already seen the property.

BHNI17

This is something else for which you might need cash on hand, or a larger loan, or a concession from the buyer. It is fairly typical for buyers to want to make some changes immediately. Some changes are optional, but some are not. Students can provide some examples. Students could make a list of possibilities and sort them into expensive versus cheap repairs, as a reality check.

BHNI18

This is a setup. The inexpensive house will turn out to need a lot of repairs. At this point students could calculate what income and cash on hand would probably be needed to purchase this house.

BHNI19

So there is a $38,500 difference between these houses. How does that translate into monthly payments? How about cash needed at the outset?

Here are the property listing sheets for each house:
Antique Cape
Ranch

Students can use these to compare the houses.

BHNI20

Repairs should include at the minimum, foundation, exterior wall, bathroom. You can't tell if it has a kitchen.

What do students think of the phrase “opportunity to continue to renovate”? The initial “renovation” meant putting a hole in the wall!

BHNI21

Evidence of a kitchen. It probably has a bathroom too. This is the difference between “you might WANT to renovate” versus an “opportunity to continue to renovate”. You can actually live in this house. How would students value the difference? The value would have to include the cost of renting while repairing the inexpensive cape.

BHNI22

If students have done the credit card module or the car purchase module, they should be able to describe the effects on total cost of long versus short term loans. They should also be able to comment on the effects of a larger down payment and different interest rates.

The spreadsheet allows students to determine a monthly payment based on the loan amount, annual interest, and length of the loan. It includes input boxes for selling price and downpayment. However, points are not incorporated in the spreadsheet.

BHNI23

Have the students try different scenarios. What else might a buyer want to reserve money for? Emergency funds, for example.

BHNI24

The calculator allows comparison between two scenarios for a loan of $200,000. One is paying no points and getting 6.5% interest. The other is paying 2 points at the outset and getting 6% interest. Of course all of the rates can be reset as needed. But the example shows that after 10 years, you have saved over $3000. Be sure to ask to view the report.

Once students understand the example on the calculator, have them do the problem on the slide.

BHNI25

It would be good at this point to revisit the “expense ratio”.

BHNI26

Have them do this in groups, each group with a different interest rate and points. For each answer, what would the monthly income have to be to support that decision? For each answer, what is the total amount paid for the house in the end?

BHNI27

For an adjustable rate mortgage, you can only calculate what the payments will be for the fixed rate period. So it is impossible to calculate what the payments will be in 4 years on a 3/1 ARM. After year 3, you don't even know what the rate will be next year.

Under what circumstances might an ARM be a good deal? What if you know you will want to sell the house in 5 years? Or what if you are waiting for another property to sell, which will pay off the house? Or what about refinancing after 3 years to a fixed rate mortgage? All of these are possibilities and ideas for student projects.

Here is a graph of how the index behaved from 1998 to 2008:

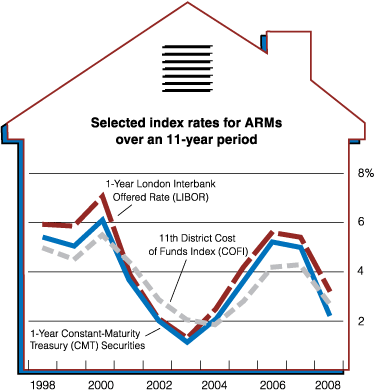
BHNI28

To wrap up, ask the students to explain what happened to the buyer in this video in math terms. Something happened to her expense ratios. What do you suppose the bank took into account when letting her mother cosign the loan? If the students were bankers, what would they want to see? You would hope they would say something about the combined expenses of mother and daughter versus the combined incomes of both. You could even have a guest banker come for the discussion or send the students to the bank to find out.

At this point the students should be ready to consider the case study and accompanying spreadsheet.