Description and Requirements
The Book
Bibliography
Syllabus
 Introduction
Introduction The Great Pyramid
The Great Pyramid Music of the Spheres
Music of the Spheres  Number Symbolism
Number Symbolism  Polygons and Tilings
Polygons and Tilings  The Platonic Solids
The Platonic Solids  Roman Architecture
Roman Architecture  Number Symbolism
Number Symbolism in the Middle Ages
 The Wheel of Fortune
The Wheel of Fortune  Celestial Themes in Art
Celestial Themes in Art  Origins of Perspective
Origins of Perspective  What Shape Frame?
What Shape Frame?  Piero della Francesca
Piero della Francesca Leonardo
Leonardo  Façade measurement by Trigonometry
Façade measurement by Trigonometry  Early Twentieth Century Art
Early Twentieth Century Art  Dynamic symmetry & The Spiral
Dynamic symmetry & The Spiral  The Geometric Art of M.C. Escher
The Geometric Art of M.C. Escher  Later Twentieth Century Geometry Art
Later Twentieth Century Geometry Art  Art and the Computer
Art and the Computer  Chaos & Fractals
Chaos & Fractals
POLYHEDRA & PLAGIARISM
in the RENAISSANCE

Slide 14-1a: The Regular Solids, one of Leonardo's Illustrations for Pacioli's Divina proportione, Reti p. 70.
Piero della Francesca was one of the most original men of the renaissance. Piero had two passions - art and geometry - the very things that this course is dealing with. He carried these on at the same time and, we will try to show here, how he integrated the two.
Luca Pacioli (c.1445-1517) was a renowned mathematician, captivating lecturer, teacher, prolific author, religious mystic, and acknowledged scholar in numerous fields. He was a link between the Early Renaissance of Piero and the High Renaissance of Leonardo.
Leonardo (1452-1519) is considered by many the ultimate renaissance man, skilled in mathematics, philosophy, civil and military architecture, engineering, painting, sculpture, science, music, invention, and the design of weapons. We'll consider Leonardo in our next unit.
These three Renaissance men were linked as student to teacher; Piero taught mathematics to Luca, and Luca taught Leonardo. They are also linked by the Platonic solids.
| Outline: | |
| Piero della Francesca | |
| de Abaco and Mathematical Education in the Renaissance | |
| Six Paintings by Piero | |
| De Quinque Corporibus Regolaribus | |
| Luca Pacioli | |
| Polyhedra & Plagiarism |
Piero della Francesca

Slide 14-1: Statue of Piero in Sansopolcro, Piero's birthplace.
Piero della Francesca (1420-1492) had two passions - art and geometry. He sought that link between an organic and geometric basis of beauty, what Kenneth Clark has called the Philosopher's stone of aesthetics.
De Prospectiva pingendi
Piero was one of the greatest practitioners of linear perspective, and even wrote a book on perspective, De Prospectiva pingendi (c.1474). This was his first of three books, the others were Trattato del abaco, and De quinque corporibus regularibus, both of which we'll mention later.
Piero wrote his book on perspective thirty-nine years after Alberti's Treatise on Painting of 1435. It is considered as an extension of Alberti's, but is more explicit. Piero was evidently familiar with Euclid's Optics, as well as the Elements, whose principles he refers to often. Theory is fine, but did Piero practice what he preached? According to Martin Kemp,
"The evidence of his paintings suggests that he did exercise an . . . extraordinary degree of meticulous, time-consuming, geometrical care over the perspectival projection of architectural forms. . ."
The Flagellation of Christ

Slide 14-2: Flagellation of Christ, c. 1460
Let's pick up the thread with Piero's Flagellation, the slide with which we closed the unit on perspective. Talking about this painting, done fourteen years before he wrote his book on perspective, Kemp says,
"No picture could exude a more pronounced air of geometric control and no painting was ever more scrupulously planned."
This painting has been analyzed to death, and I even have a computer analysis locating the vanishing point to the nearest millimeter, in a painting that is 81,500 mm by 59,000 mm.
If you extend the orthogonals to locate the vanishing point, it does not seem to fall on any point that is significant to the story. But Kemp shows that point does have geometric significance.
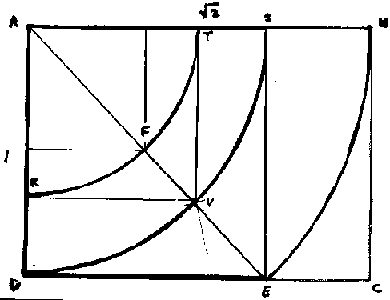
Slide: Geometry of the Flagellation
He gets his clue from the dimensions of the painting; 58.4 cm (one braccio) by 81.5 cm., giving the ratio of the sides = 1.40 ~ 21/2. If we swing arc EB from A, we get a square ASED. Thus the width of the painting equals the diagonal of the square, verifying that the frame is a root-two rectangle.
The diagonal AE of that square passes through the V, vanishing point of perspective.
Further, in square ATVK we see that arc KT from A cuts the diagonal at Christ's head, F, halfway up the painting. Thus Christ's head is at the center of the original square ASED.
The Tile patterns:
Christ stands on a simple green circle, inscribed in a square. A case of squaring the circle?
Kemp points out that the tile pattern inside the praetorium is complex, and based on the diagonal of a square, an irrational number such as found in the proportions of the frame. The tile pattern outside the praetorium is simple squares, in an Albertian grid, and there is no apparent correlation between them. This seems to create two separate zones: the space inside, occupied by Christ, and the more mundane world outside. Deliberate? Kemp says that for someone as subtle as Piero, this is not impossible.
Further, the tiles inside the praetorium form an octagonal pattern. Recall from our unit on number symbolism that the octagon suggests resurrection and baptism, because Christ rose from the tomb eight days after entering Jerusalem.
de Abaco and Mathematical Education in the Renaissance
That was pretty subtle geometry in the Flagellation. Could a Renaissance viewer really appreciate all that? How much mathematics did the average person know?
In Renaissance Florence, according to Baxandall, a boy was educated in two stages. For about four years, from age six or seven, he learned reading, writing, and business correspondence. Then for another four years most would go to a secondary school, the abbaco (which means arithmetic), where they learned mostly mathematics, especially commercial mathematics adapted to the merchant.
One of the books used in these schools was Piero's second book, de abaco.
Proportion and the Rule of Three:
One important subject was how to solve proportions, crucial to a merchant who had to deal with problems of pasturage, brokerage, discount, tare allowance, adulteration of commodities, barter, and currency exchange. Not only did every city have its own currency, but its own weights and measures!
The universal mathematical tool of literate commercial people in the Renaissance was the Rule of Three, also called the Golden Rule and the Merchant's Key. In his Del abaco, Piero explains how to use the rule of three to solve a proportion:
"multiply the thing one wants to know about
by the thing that is dissimilar to it,
and divide by the remaining thing.
The result is dissimilar to the thing we want to know about."
Example: If seven bracci (1/3 person's height or about 23") of cloth are worth nine lire; how much will five bracci of cloth be worth?
Solution:
The thing we want to know about is: 5 bracci of cloth.
So: (5 bracci) x (9 lire) / (7 bracci) = 6 3/7 lire
The units are lire, because lire are dissimilar to bracci, the units in the thing we wanted to know about.
Skills in Proportion Affected the Way People Saw Pictures
So what does ability to solve proportions have to do with art? Baxandall claims that the skills used to solve exchange problems were the same used for the making or seeing of pictures.
He makes the following points:
1. Renaissance education placed exceptional value on a few math skills, like proportion. People didn't know more math than we do, but they knew it absolutely; it was a relatively larger part of their intellectual equipment.
2. The math skills used by merchants were the same as those used by the painter.
3. The status of these skills in his society was an encouragement to the painter to assert them in his pictures.
4. Because merchants were practiced in manipulating ratios, they were sensitive to pictures carrying the marks of similar processes. It was a small step from the proportions of a currency exchange to the proportion of a physical body, such as the cup and the fish in the slide, to the proportions of a man's head, as done by Leonardo in this sketch from his notebooks, or by Piero in his Flagellation.
Familiarity with Gauging Affected the Way People Saw Pictures
Standard sized containers date only from the nineteenth century, so quick calculation of volumes of barrels, sacks, piles of grain, etc., called gauging, was a condition of business.
In the 15th century German merchants used
complex prepared rulers. An Italian used geometry and
 ,
and Piero's De abaco
gives methods and exercises for these computations.
,
and Piero's De abaco
gives methods and exercises for these computations.
As with proportion, according to Baxandall, skill at gauging affected art. The ability of a merchant to break down complex shapes into simpler geometrical units is similar to the way a painter or sculptor analyzes shapes.
Painters and merchants had received the same mathematical education; this was the geometry they knew and used. So the literate public had the same geometrical skills with which to view paintings,
and the painters knew this. We'll see a good example in Piero's Vision of Constantine.
Six Paintings by Piero
In this section we'll look at six paintings by Piero and, for each, try to point out anything of geometric interest.
Nativity

Slide 14-2a: The Nativity, Piero della Francesca, 1472-4
Square Format Arrests Motion: Remember from our first session how the square format tended to make a scene static and solemn? Arnheim notes that here the square format turns story of the Adoration into a solemn group portrait.
Axes of Symmetry: We have noted earlier, in Raphael's Knights Dream and Munch's Sick Girl, for example, that the axes of symmetry of square format often used to divide zones. Here, the central vertical divides scene into two groups; angelic musicians on left, Holy Family and shepherds on right. The two groups do not interact.
Resurrection of Christ

Slide 14-3: The Resurrection of Christ, Piero della Francesca, 1460-63 (Cat. 19806)
We see that Piero was fond of the square format. Here's another example, for this painting is essentially square, being about 10% higher than it is wide.
Stillness: The square format, as we've seen before, gives a mood of overall stillness. This static quality is enhanced by locating Christ exactly on center. Arnheim says that Christ's frontal symmetry makes him look like a statue. Christ is static but the guards appear restless. Their tilted heads are a perfect foil for the riveting head of Christ.
Vertical Zones: The central vertical divides the scene with Winter on left, summer on right. The rebirth of nature is here probably a symbol for rebirth of Christ.
Horizontal Zones: Similarly, the painting is divided into three horizontal bands. Christ occupies the middle band, his head and shoulders reaching into the upper band of sky. His figure unites earth and the heaven. The guards are in the zone below the line marked by Christ's foot.
Baptism of Christ

Slide 14-4: Baptism of Christ, priory of San Giovanni, Sansopolcro. c. 1450 (Cat. # 2690)
Arnheim points out the following:
* A microtheme, baptism bowl near center of picture.
* Severely foreshortened dove at center of circle and top of square. lends a mystical touch.
* Frozen, static quality found in square pictures, or in round pictures.
* The tree trunk is at 1/3 the width, the dove is at 1/3 the height.
* Piero's home town of Sansopolcro can be seen in the distance, between Christ and the tree.
* John's arm and Christ's loincloth continue the line of the circle.
* Square and circle overlap, like the circles in a vesica, with Christ in area common to both. If the circle is equated with heaven, and the square with earth, here Christ is shown as mediator between the two. Here Piero has combined squaring the circle and the Vesica in one painting
* The recurring motif of the three graces.
* Figures are simplified, cubist, geometric. Piero has been called "the first cubist."
The Introducer

Slide 14-5: Baptism. Closeup of the angels
Recall that Alberti, in his Della pittura, gives some suggestions for history paintings, or istoria.
". . . I like there to be someone in the 'istoria' who tells the spectators what is going on, and either beckons them with his hand to look, or with ferocious expressions and forbidding glance challenges them not to come near, as if he wished their business to be secret, or points to some danger or remarkable thing in the picture, or by his gestures invites you to laugh or weep with them."
In the Baptism, this role is filled by the three angels, one of whom makes eye contact with the viewer.
Madonna del Parto

Slide 14-6: C. 1496. Fisher p. 47
Piero's fondness for the square format and for symmetry is again shown here. Note the two angels are practically mirror images.
Vision of Constantine

Slide 14-7: Vision of the Emperor Constantine, from Legend of the True Cross, c. 1450. S. Francesco, Arrezo (Cat. 2449)
According to Baxandall, an obvious way for a painter to invoke the gauger's response was to use the repertory of stock objects from gauging exercises - cisterns, columns, towers, paved floors, and so on.
Almost every math handbook had an exercise to compute the surface area of a conical tent like the one in this painting, to find the amount of cloth needed to make it. A painter who left traces of such analysis was leaving cues that his public was well equipped to pick up. Also, the geometric figure functions as an Albertian mediator between artist and merchant, a similar function performed by the angel in the Baptism, and by the seated man in this painting.
Also, the tent pole and the horizontal band on the tent form a Latin cross, another familiar shape to act as mediator.
Also noteworthy is:
the highly foreshortened angel, who enters the scene from the viewer's space.
Light bursts from him bathing the scene.
Night scenes were very rare in painting at this time.
Piero's last known painting

Slide 14-8: Virgin and Child with Saints, Angels, and Federigo da Montefeltro, 1472-4, 248 x 170 cm. Beirati p. 86 (Cat. # 6460)
This painting was commissioned by Federigo, Duke of Urbino, for a new chapel after the death of his young (26 years) wife Battista Sforza. She would ordinarily be kneeling opposite Federigo, and in front of her namesake John the Baptist, but is absent.
A mysterious ostrich egg hovers above, the way the dove hovered over Christ in the Baptism. Such an egg often hangs over alters dedicated to the Virgin. It was believed that the ostrich let her egg hatch in the sunlight without intervention, and thus became a symbol of virgin birth. Also, the ostrich is here an absent mother, a symbol of the deceased Battista.
The vanishing point is on the Virgin's head. Geometrically, the ratio of width to height is 2:3, a musical ratio. This same ratio appears in the vault, which has 6 coffers in one direction and 9 in the other. The ratio of the diameter of the circle of the vault to a circle inscribed in the lower part of the picture is also 2:3.
De Quinque Corporibus Regolaribus

Slide 14-9: Madonna and Child with Saints and Angels, detail showing Pacioli.
Twenty years before his death in 1492, Piero is said to have given up his highly successful career in painting and devoted himself entirely to mathematics. This may have been due to failing sight. Vasari says that Piero went blind at about age 60, (c.1480).
It was during this period that he wrote his three math books, the two already mentioned, and his last, on the five regular solids, De quinque corporibus regularibus, described by Plato in his Timaeus.
Piero's book was never published but was placed in the library of Federigo da Montefeltro, seen kneeling in this painting. Unfortunately the work was plagiarized. By whom? By another man in this same painting, Piero's student, Luca Pacioli!
Luca Pacioli

Slide 14-10 Portrait attributed to Jacapo de' Barberi, closeup. Lawlor cover
Luca Bartolomes Pacioli (c.1445-1517) was a renowned mathematician, captivating lecturer, teacher, prolific author, religious mystic, and acknowledged scholar in numerous fields. He was a link between the Early Renaissance of Piero and the High Renaissance of Leonardo.
Luca's Connections to Piero
Luca and Piero were close. Both were born in Sansopolcro, and Luca was tutored in mathematics by Piero. Luca even posed for Piero in the mid 1470's for Madonna and Child with Saints and Angels, in which Pacioli portrays St. Peter Martyr, with cut head symbolizing his assassination.
Piero and Luca sometimes walked across the Apennines to the library of Duke Federigo of Urbino, which was then one of the finest in Europe. Raphael may have been thinking about that library, with portraits of the writers above their works, when he painted the School of Athens.
Luca's Connections to Alberti
Piero introduced Luca to Alberti, who arranged for Pacioli's first teaching job, tutor for the three sons of a wealthy Venetian. Alberti, the champion of the Italian vernacular, urged that Pacioli write about mathematics in that language. Alberti had belief in the cosmic significance God-given validity of musical ratios, and this belief was carried on by Pacioli
The Summa
In 1472, shortly after Alberti's death, Pacioli took vows, and is usually shown in paintings in a Franciscan habit. Luca lectured in math in Perugia (1475). He then he took to the road (c.1475-1497) and became traveling teacher of mathematics, giving sermons, writing.
He published the Summa de arithmetica, geometrica, proportioni et proportionalita (1494 ) a summary of arithmetic, geometry, and algebra, the sort of book a weak student now uses in a remedial math course. It was one of the first books to be printed in Venice by the new Gutenberg method. It contains the first mention of double-entry book-keeping, for which Luca is now known as the "Father of Accounting."
Luca's Connections with Leonardo
In 1497 Leonardo da Vinci, impressed by the Summa, apparently encouraged Sforza to bring Pacioli to Milan to tutor him in mathematics, geometry, and proportion. They stayed together for 10 years, in Milan and Florence. Pacioli is mentioned several times in Leonardo's notebooks of this period., and Leonardo got his knowledge of perspective from Piero through Pacioli.
Luca went to Pisa in 1500 , lectured on Euclid, and in 1509 produced a Latin edition of Euclid, based on Euclid's Thirteenth book of Elements. In his portrait attributed to Jacopo de' Barbieri, Pacioli's hand rests on the Thirteenth book of Euclid.
The Divina Proportione
Luca published the Divina proportione in 1509. He wrote it in the Italian vernacular, as urged by Alberti. In it he refers to the golden ratio "dal ciel mandata" - heaven-sent. Why does he call the golden ratio divine?
1. Like God, it is unique.
2. As the Trinity is one substance in three persons, the divine proportion is a single proportion in three terms.
3. As God cannot be described in words, the divine proportion cannot be expressed by a rational number. It is occult and secret (secretissima scientia).
4. Like God it is always similar to itself.
So after centuries of oral transmission, the golden ratio is finally pinned down in writing.
And what happened? Everyone seemed to lose interest in it.
According to Bouleau, "Perhaps the turning of a bright light upon old secrets is the annunciation of their death. In fact, it marked the beginning of the decline. The divine proportion had lost its magical attraction ... "
Lettering
The second main topic in his De divina Proportione was classical Roman lettering. It was addressed to stone cutters and builders, and probably influenced later similar works by Dürer and Geofroy Tory.

Slide 14-11 Platonic Solids from Pacioli Show
Pacioli devoted the entire second part of Divina Proportione to the Platonic solids, relating the Platonic solids to the golden ratio like this:
"As God brought into being the celestial virtue, the fifth essence, and through it created the four solids . . . earth, air, water, and fire ... so our sacred proportion gave shape to heaven itself,
in assigning to it the dodecahedron . . . the solid of twelve pentagons, which cannot be constructed without our sacred proportion. As the aged Plato described in his Timaeus."
Here Luca equates God with Plato's divinity, and wraps up the Platonic solids, the golden ratio, the creation of the universe, and God, into one neat package.
Luca credits Leonardo with the illustrations in De divina proportione. He writes,
"the most excellent painter in persective, architect, musician, and man de tutte vertu doctato, Leonardo da Vinci, who deduced and elaborated a series of diagrams of regular solids ... "
This section of the book has little relation to the earlier part and was apparantly stolen from Piero and tacked on, without credit. Vasari (1550) had some harsh words for the good friar.
"The man who should have tried his best to increase Piero's glory and reputation (since he learned everything he knew from him), instead wickedly and maliciously sought to remove his teacher Piero's name and to usurp for himself the honour due to Piero alone by publishing under his own name - that is, Fra Luca Pacioli, all the efforts of that good old man ... "
Reading
De prospectiva pingendi
De abaco and Mathematical education in the Renaissance
Gauging
De quinque corporibus regularibus
Vasari's chapter on Piero della Francesca
Pedoe, pp. 82-101
Panofsky pp. 129-138
Kemp pp. 27-35
Cole, pp. 18, 19, 24, 25, 28
Reti, 56-85, 216-239
Baxandall, Part II, Sections 9-11 (pp. 86-108) Baxandall, 109-152
Tinius and Weis paper
