Description and Requirements
The Book
Bibliography
Syllabus
 Introduction
Introduction The Great Pyramid
The Great Pyramid Music of the Spheres
Music of the Spheres  Number Symbolism
Number Symbolism  Polygons and Tilings
Polygons and Tilings  The Platonic Solids
The Platonic Solids  Roman Architecture
Roman Architecture  Number Symbolism
in the Middle Ages
Number Symbolism
in the Middle Ages  The Wheel of Fortune
The Wheel of Fortune  Celestial Themes in Art
Celestial Themes in Art  Origins of Perspective
Origins of Perspective  What Shape Frame?
What Shape Frame?  Piero della Francesca
Piero della Francesca  Leonardo
Leonardo  Façade measurement
Façade measurement  Early Twentieth Century
Art
Early Twentieth Century
Art  Dynamic symmetry &
The Spiral
Dynamic symmetry &
The Spiral  The Geometric Art
of M.C. Escher
The Geometric Art
of M.C. Escher  Later Twentieth Century
Geometry Art
Later Twentieth Century
Geometry Art  Art and the Computer
Art and the Computer  Chaos & Fractals
Chaos & Fractals
The Golden Ratio &
Squaring the Circle
in the Great Pyramid
"Twenty years were spent in erecting the pyramid itself: of this, which is square, each face is eight plethra, and the height is the same; it is composed of polished stones, and jointed with the greatest exactness; none of the stones are less than thirty feet." -Herodotus, Chap. II, para. 124.

Slide 2-1: The Giza Pyramids and Sphinx as depicted in 1610, showing European travelers Tompkins, Peter. Secrets of the Great Pyramid. NY: Harper, 1971. p. 22
| Outline: | The Great Pyramid |
| The Golden Ratio | |
| Egyptian Triangle | |
| Squaring the Circle | |
| Rope-Stretcher's Triangle | |
| Summary |
The Great Pyramid
 |
Slide 2-2: The Great Pyramid of Cheops
Tompkins, Peter. Secrets of the Great Pyramid. NY: Harper, 1971. p. 205 |
We start our task of showing the connections between geometry, art, and architecture with what appears to be an obvious example; the pyramids, works of architecture that are also basic geometric figures.
The pyramids were built in the lifetime of a single king, and were to help him in become immortal. They were made mostly in 4th dynasty of the old kingdom, about 2800 B.C.
Herodotus
 |
Slide 2-4: Herodotus
Encarta ‘96 Encyclopedia. Funk and Wagnalls, 1995. |
Herodotus (484?-425 BC), called the Father of History, was the first to write about the pyramids around 440 B.C.
In his History Herodotus says that the pyramids, already ancient, were covered with a mantle of highly polished stones joined with the greatest exactness.
Secrets of the Great Pyramid
The pyramids are claimed to have many "secrets;" that they are models of the earth, that they form part of an enormous star chart, that their shafts are aligned with certain stars, that they are part of par of a navigational system to help travelers in the desert find their way, and on and on.
In this unit we'll examine the claim that the Great Pyramid contains the Golden Ratio, whatever that is, and then look at the claim that the Great Pyramid squares the circle, whatever that is.
Golden Ratio
So what is this Golden Ratio that the Great Pyramid is supposed to contain?
A ratio is the quotient of two quantities. The ratio of a to b is
a/b
The price/earnings ratio is the price of a share of stock divided by the earnings of that share.
Price/ Earnings
A proportion results when two ratios are set equal to each other. Thus if the ratio of a to b equals the ratio of c to d, we have the proportion,
a/b = c/d
Systems of ProportionsThroughout much of art history, artists and architects were concerned with the proportions of the parts of their works. For example, if you were designing a temple, you might want to make the ratio of its height any old number, or perhaps, for some reason, a particular value. In fact, we'll see that there were not only particular ratios that were preferred, but sometimes entire systems of proportions.
Some systems of proportions were based on:
1. The musical intervals
2. The Human Body
3. The Golden Ratio
We'll see as we go along that these systems of proportions will be recurring themes thoughout the course.
Definition of the Golden Ratio
The golden ratio is also called extreme and mean ratio. According to Euclid,
A straight line is said to have been cut in extreme and mean ratio when, as the whole line is to the greater segment, so is the greater to the less.
Derivation of the Golden Ratio
Let smaller part = 1, larger part = ![]() . Thus
. Thus ![]() is the golden
ratio. It is often designated by the greek letter phi,
is the golden
ratio. It is often designated by the greek letter phi,
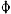 for Phideas, (fl. c. 490-430 BC),
Athenian sculptor and artistic director of the construction of the
Parthenon, who supposedly used the golden ratio in his work.
for Phideas, (fl. c. 490-430 BC),
Athenian sculptor and artistic director of the construction of the
Parthenon, who supposedly used the golden ratio in his work.
Then by the definition of the golden ratio,
![]() / 1 = (1 +
/ 1 = (1 + ![]() ) /
) / ![]()
so
![]() 2 = 12 + 1
2 = 12 + 1![]()
and we get the quadratic equation,
![]() 2 -
2 - ![]() - 1 = 0
- 1 = 0
As a project, solve this quadratic equation for the golden ratio ![]() . You should get,
. You should get,
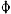 = 1/2 +
= 1/2 +  5 / 2
5 / 2  1.618
1.618
Project: Do this derivation.
Geometric Construction of the Golden Ratio
Subdivide a square of side 1 into two equal rectangles. Then lay out a distance equal to the diagonal of one of these half-squares, plus half the side of the original square. The ratio of this new distance to the original side, 1, is the golden ratio.
Project: Do this construction for the golden ratio.
Project: Mathematically show that this construction gives the golden ratio.
Egyptian Triangle
Let's now return to the pyramids. If we take a cross-section through a pyramid we get a triangle. If the pyramid is the Great Pyramid, we get the so-called Egyptian Triangle. It is also called the Triangle of Price, and the Kepler triangle.
This triangle is special because it supposedly contains the golden ratio. In particular,
the ratio of the slant height s to half the base b is said to be the golden ratio.
To verify this we have to find the slant height.
Computation of Slant Height s
The dimensions, to the nearest tenth of a meter, of the Great Pyramid of Cheops, determined by various expeditions.
Half the base is
230.363 ÷ 2 = 115.182 m
So,
s 2 = 146.515 + 115.182 2 = 34,733 m2
s = 18636.9 mm
Does the Great Pyramid contain the Golden Ratio?Dividing slant height s by half base gives
which differs from ![]() (1.61803) by
only one unit in the fifth decimal place.
(1.61803) by
only one unit in the fifth decimal place.
The Egyptian triangle thus has a base of 1 and a hypotenuse equal to
![]() . Its height h,
by the Pythagorean theorem, is given by
. Its height h,
by the Pythagorean theorem, is given by
h2 = ![]() 2 - 12
2 - 12
Solving for h we get a value of

![]() .
.
Project: Compute the value for the height of
the Egyptian triangle to verify that it is

![]() .
.
Thus the sides of the Egyptian triangle are in the ratio

Kepler Triangle
The astronomer Johannes Kepler (1571-1630) was very interested in
the golden ratio. He wrote,
"Geometry has two great treasures: one is the theorem of Pythagoras,
the other the division of a line into mean and extreme ratios, that is
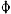 , the Golden Mean. The first way may be compared
to a measure of gold, the second to a precious jewel."
, the Golden Mean. The first way may be compared
to a measure of gold, the second to a precious jewel."
In a letter to a former professor he states the theorem, which I rephrase as:
If the sides of a right triangle are in geometric ratio, then the sides are

We recognize this as the sides of the Egyptian triangle, which is why its also called the Kepler triangle.
Project: Prove that If the sides of a right triangle are in geometric ratio, then the sides are

A British railway engineer, Robert Ballard, saw the pyramids on his way to Australia to become chief engineer of the Australian railways. He watched from a moving train how the relative appearance of the three pyramids on the Giza plateau changed. He concluded that they were used as sighting devices, and wrote a book with the grand title of The Solution of the Pyramid Problem in 1882.
He also noted that the cross-section of the Great Pyramid is two of what we have called Egyptian triangles. He then constructs what he called a Star Cheops, which, he says, "... is the geometric emblem of extreme and mean ratio and the symbol of the Egyptian Pyramid Cheops."
To draw a star Cheops:
- Draw vertical and horizontal axes.
- Using their intersection as center, draw two circles, radius 1, and radius 1 +
 .
. - Superscribe a square about the smaller circle. This will be the base of the pyramid,
- From the point where an axis cuts the outer circle, draw two lines to the corners of the square. The triangle obtained will be one face of the pyramid.
- Repeat the preceding step for the remaining three faces, getting a four-pointed star. Cut it out.
- Fold each triangular face up from the base forming the pyramid.
Project Draw a star Cheops. Fold it to quickly make a model pyramid.
Squaring the Circle
 |
Slide 2-3: The Great Pyramid
National Geographic. April '88 |
Now we'll look at his other claim, that the Great Pyramid's dimensions also show squaring of the circle. But just what is that?
The problem of squaring the circle is one of constructing, using only compass and straightedge;
(a) a square whose perimeter is exactly equal to the perimeter of a given circle, or
(b) a square whose area is exactly equal to the area of a given circle.
There were many attempts to square the circle over the centuries, and many approximate solutions, some of which we'll cover. However it was proved in the ninteenth century that an exact solution was impossible.
Squaring of the Circle in the Great Pyramid
The claim is:
The perimeter of the base of the Great Pyramid equals the circumference of a circle whose radius equal to the height of the pyramid.
Does it? Recall from the last unit that if we let the base of the Great pyramid be 2 units in length, then
pyramid height = 
So:
Perimeter of base = 4 x 2 = 8 units
Then for a circle with radius equal to pyramid height
 .
.


 7.992
7.992So the perimeter of the square and the circumference of the circle agree to less than 0.1%.
An Approximate Value for
 in Terms of
in Terms of
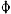
Since the circumference of the circle (2 
 )
nearly equals the perimeter of the square (8)
)
nearly equals the perimeter of the square (8)


 8
8we can get an approximate value for  ,
,

 4 /
4 /
 = 3.1446
= 3.1446which agrees with the true value to better than 0.1%.
Area Squaring of the Circle
The claim here is:
The area of that same circle, with radius equal to the pyramid height equals that of a rectangle
whose length is twice the pyramid height(
![]() ) and whose width is the width (2) of the pyramid.
) and whose width is the width (2) of the pyramid.
Area of rectangle = 2 ( ) ( 2 ) = 5.088
) ( 2 ) = 5.088
Area of circle of radius  =
=  r 2
r 2 
 (
( ) 2
) 2

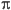
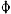 = 5.083
= 5.083
an agreement withing 0.1%
The Pizza-Cutter Theory
Suppose that the Egyptians didn't know anything about but laid out the pyramid using a measuring wheel, such as those used today to measure distances along the ground.
Take a wheel of any diameter and lay out a square base one revolution on a side. Then make the pyramid height equal to two diameters
By this simple means you get a pyramid having the exact shape of the Great Pyramid containing perimeter-squaring of the circle and area squaring of the circle and, for no extra cost, the golden ratio!
Project: Use a pizza cutter or a similar disk to construct a pyramid similar to the Great Pyramid.
Project: Show, by calculation, that using a measuring wheel as described will give a pyramid of the same shape as the Great Pyramid.
Project: Find the diameter of the measuring wheel required so that:
100 revolutions = the base of the Great Pyramid
200 diameters = the height of the Great Pyramid
We'll see that this idea of squaring the circle will be a recurring theme throughout most of this course. But lets leave it for now and get back to triangles.
Rope-Stretcher's Triangle
One practical value of any triangle is its rigidity. A triangular frame is rigid, while a four-sided one will collapse.
Another imortant use is for triangulation, for locating things as in surveying and navigation, and this property takes us back to the very origins of geometry, in ancient Egypt.
The Origins of Geometry
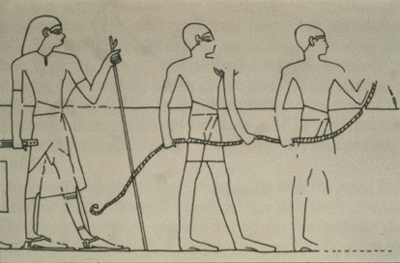 |
Slide 2-5: Hardenonaptai: Rope stretchers or engineers
Tompkins, Peter. Secrets of the Great Pyramid. NY: Harper, 1971. p. 22 |
Geometry means earth measure. Geo + Metry. According to the Herodotus the Nile flooded its banks each year, obliterating the markings for fields.
He wrote, "This king divided the land . . . so as to give each one a quadrangle of equal size and . . . on each imposing a tax. But everyone from whose part the river tore anything away . . . he sent overseers to measure out how much the land had become smaller, in order that the owner might pay on what was left . . . In this way, it appears to me, geometry originated, which passed thence to Greece.
The Rope-stretcher's Triangle
One tool they may have used is a rope knotted into 12 sections stretched out to form a 3-4-5 triangle. Does it Produce a Right Angle?
According to the Pythagorean theorem,
In a right triangle, the square of the hypotenuse equals the sum of the squares of the legs.
The converse of is also true,
If the square of one side of a triangle equals the sum of the squares of the other two sides, then we have a right triangle.
For the 3-4-5 triangle;
52 = 32 + 42
25 = 9 + 16
It checks, showing a rope knotted like this will give a right angle.
The rope-stretcher's triangle is also called the 3-4-5 right triangle, the Rope-Knotter's triangle, and the Pythagorean triangle.
Project: Use a long knotted rope to make a rope-stretcher's triangle. Use it outdoors to lay out a right angle on some field. Then continue, making three more right angles to form a square. How accurate is your work? Did you come back to the starting point?
Summary
Was the golden ratio intentionally built into the Great Pyramid of Cheops? Why would anyone intentionally build the golden ratio into a pyramid, or other structure? What was the significance of to the Egyptians? And did the ancient Egyptians intentionally design the Great Pyramid to square the circle?
Its hard to know, but at any rate, we've introduced the golden ratio and squaring the circle themes which we'll encounter many times again in this study.
We've also some symbolism here:
If flooding of the Nile symbolized the annual return of watery chaos, then geometry, used to reestablish the boundaries, was perhaps seen as restoring law and order on earth. We'll see this notion again of geometry being sacred because it represents order, especially in the Middle Ages.
The rope stretchers triangle when opened out gives a zodiac circle, with the number of knots the most important of the astrological numbers
The square, with its four corners like the corners of a house, represents earthly things, while the circle, perfect, endless, infinite, has often been taken to represent the divine or godly. So squaring the circle is a universal symbol of bringing the earthly and mundane into a proper relationship with the divine.
And the Golden Ratio reverberates with the idea of the Golden Mean, the principle of moderation, defined by Aristotle as the mean between the two extremes of excess and insufficiency, as generosity is the mean between prodigality and stinginess, and by Horace, called the philosopher of the golden mean, advocated moderation even in the pursuit of virtue.
Remember that the pyramids were tombs, and that much of Egyptian art is funarary art. One Egyptian word for sculptor literally means He who keeps alive. To help the king acheive immortality, it was important that he didn't rot, hence the elaborate embalming. But embalming was not enough. The likeness of the king must also be preserved in gold or granite. So the tomb was seen as a sort of life insurance policy. Thus sculpture evolved.
But there is another angle to sculptor ... he who keeps alive. Once, the servants and slaves were buried with the king to help him in the other world. Then art came to the rescue, providing carved and painted substitutes for the real people. So the sculptor not only kept alive the memory of the dead king but literally kept alive all these people that would have been buried with the king.
Who says art isn't important?
 |
Slide 2-7: King Tutankhamun
Metropolitan Museum of Art Gift Catalog, The Treasures of Tutahkhamun. NY: Met 1978. |
Finally, in these units on Egypt we've started down the road that we'll follow right to the present time. The art historian Ernst Gombrich writes,
". . . the story of art as a continuous effort does not begin in the caves of southern France or among the North American Indians. . . there is no direct tradition which links these strange beginnings with our own days . . .But there is a direct tradition, handed down from master to pupil . . . which links the art of our own days with the art of the Nile valley some 5000 years ago. . .".. the Greek masters went to school with the Egyptians, and we are all the pupils of the Greeks.
In our next unit we'll cross the Mediteranean Sea where we too will be pupils of the Greeks.
Projects
Do the derivation of the golden ratio.
Do the construction for the golden ratio.
Compute the value for the height of the Egyptian triangle to verify that it is

![]() .
.
Prove that If the sides of a right triangle are in geometric ratio, then the sides are
 .
.
Draw a star Cheops. Fold it to quickly make a model pyramid.
Use a pizza cutter or a similar disk to construct a pyramid similar to the Great Pyramid.
Show, by calculation, that using a measuring wheel as described will give a pyramid of the same shape as the Great Pyramid.
Find the diameter of the measuring wheel required so that:
100 revolutions = the base of the Great Pyramid
200 diameters = the height of the Great Pyramid
Use a long knotted rope to make a rope-stretcher's triangle. Use it outdoors to lay out a right angle on some field. Then continue, making three more right angles to form a square. How accurate is your work? Did you come back to the starting point?
Reading
Markowsky, Misconceptions Concerning the Golden Ratio.
Tompkins, Chapter 16
Herodotus Book II, Paragraphs 124, 135
Euclid, Elements. P. 1, 2, Book 6, Definition 3.
Calter, pp. 156-171, pp. 548-551
