Math Art
George Hart once said that "Math is the most abstract art," and indeed few people see
the creativity and beauty in it that many mathematicians do. By combining mathematical ideas with traditional media
like sculpture and music, the broader public can appreciate this artistic side of math. In this talk,
we'll explore the uncountable ways art has been infused with math, from using DeBrujin's theorem to count
the patterns in traditional Japanese braiding, to edible polyhedra and much more!
slides
Below is some of the mathematical art I have made:



These pies are inspired by Lauren Ko, author of Piometry, whose book was helpful in making these. They are joint
work with Elizabeth Buchanan, Beth-Anne Castellano, and Alex Wilson. Each represents a
different mathematical concept.
The first is a random tiling of the "Aztec diamond" by dominos, color coded by
their orientation. One of the artic circle theorems says that a randomly selected tiling will have a circle of
randomness, surrounded by "frozen" sections at the corners, where all pieces have the same orientation.
The second is one of the pentagonal tilings discovered by Marjorie Rice, an amateur mathematician that made a massive
contribution to a longstanding problem about the possible tilings by irregular pentagons. It reminds us that everyone
can have great ideas, and that math is something for everyone.
The last pie is the aperiodic monotile discovered
by Smith, Myers, Kaplan, and
Goodman-Strauss. This tile solves the "Einstein" problem, namely it is a single tile that can only cover the
plane without any symmetries, which had been a longstanding question that ended up admitting a unexpectedly simple
solution. This too was solved by an amateur mathematician.

These shortbread cookies are 3x3 Latin and Euler squares, using different levels of chocolate to achieve the various colors
(joint baking with Beth-Anne Castellano and Matthew Ellison). They were distributed alongside a
Graduate Student Seminar
I gave about this topic.
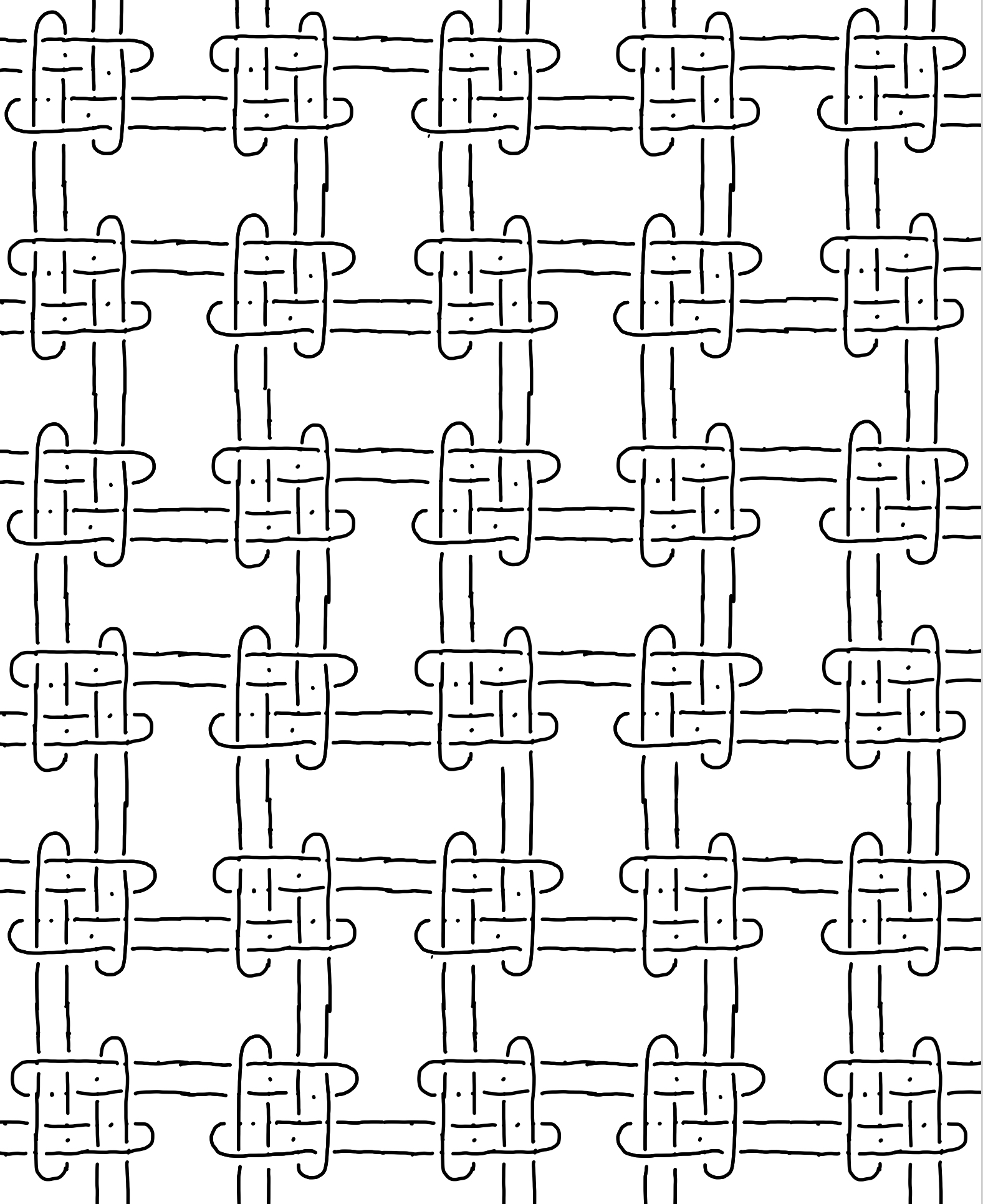

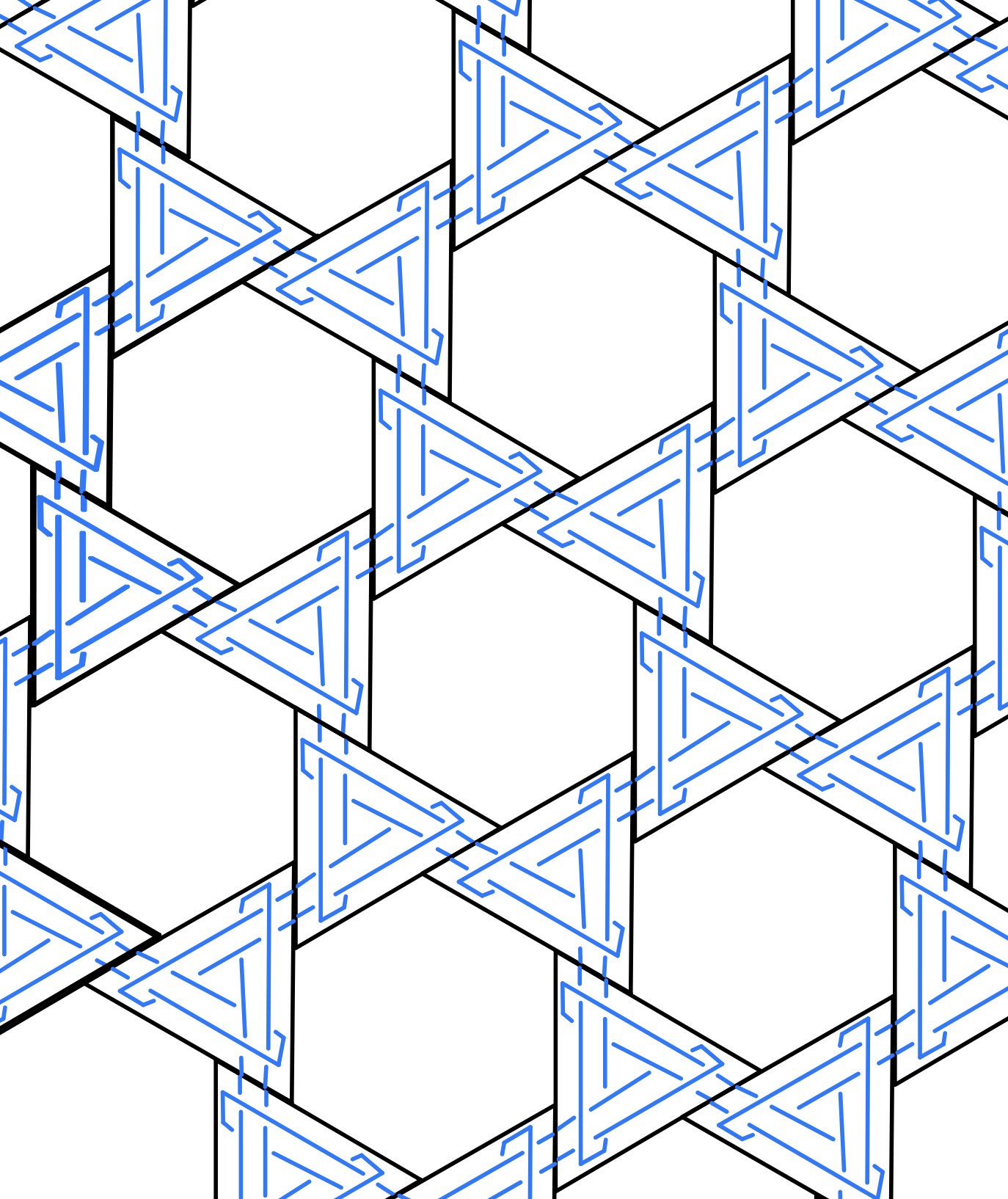

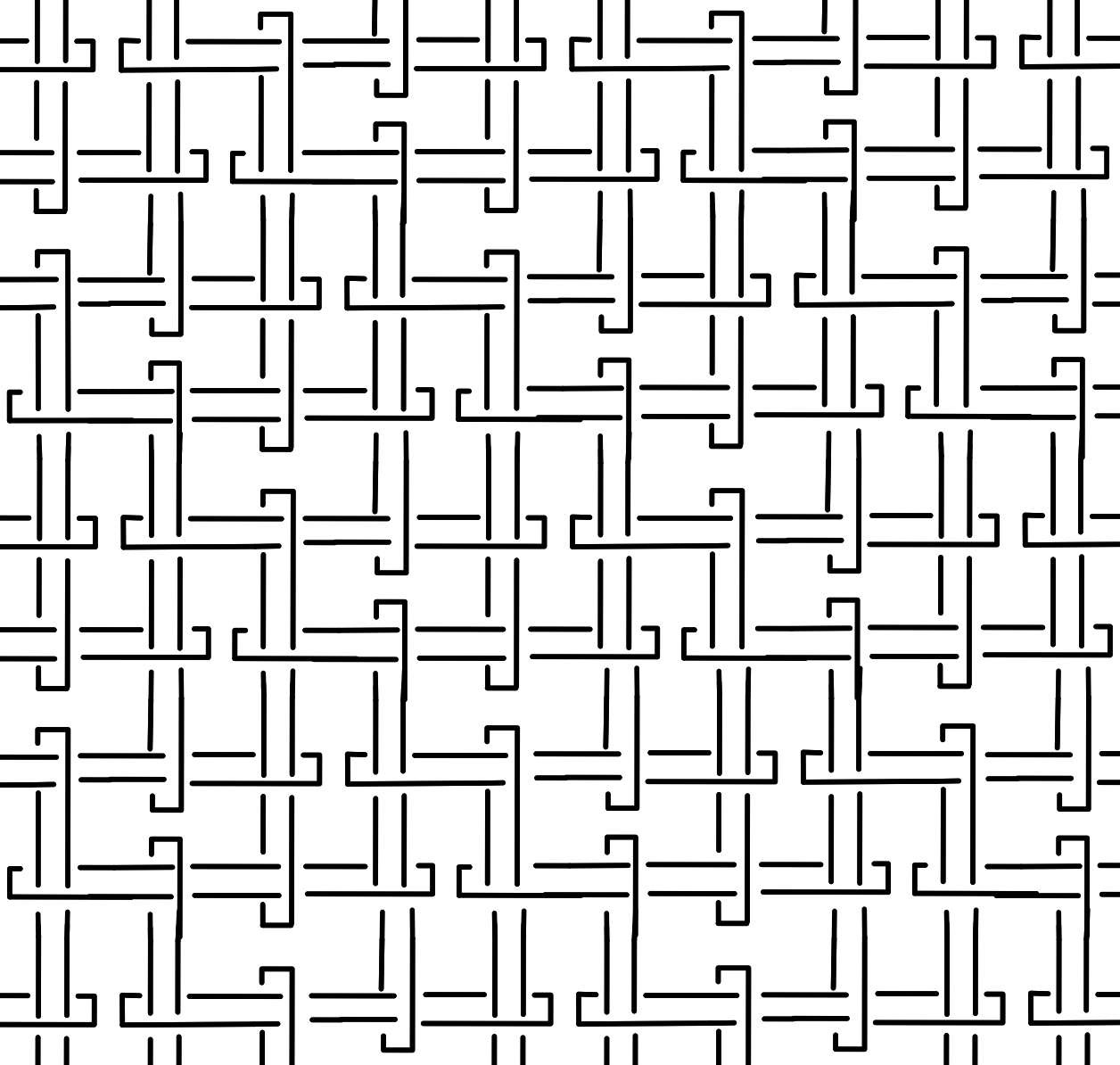
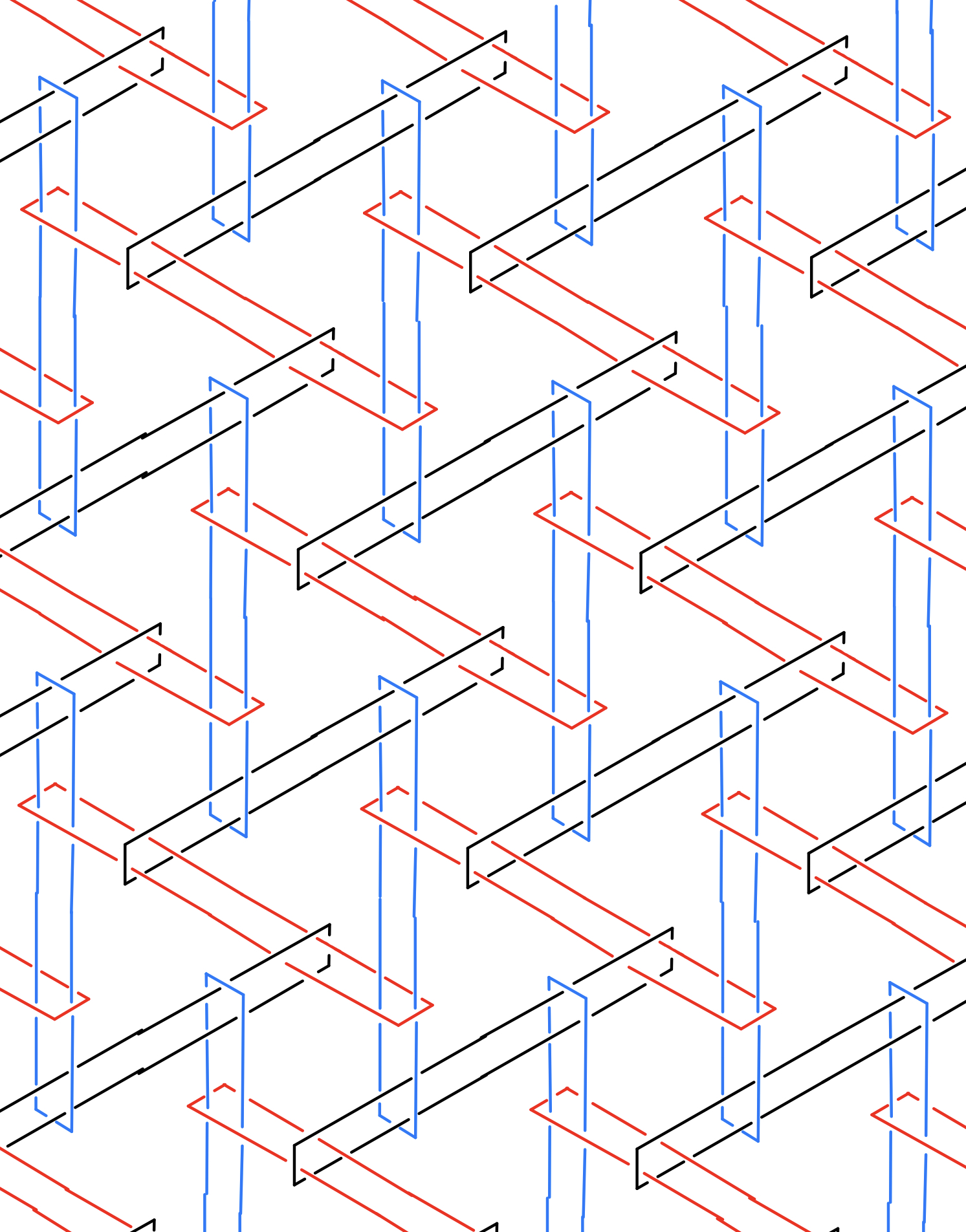
These are various 2 dimensional infinite
Brunnian links based on tiles. A link is a set of entangled circles,
and it has the "Brunnian" property if removing any single component allows one to untangle them all. These objects are therefore
rather fragile, and it's only by the delicate interplay of their components that they are kept together. A more complete description of this
topic is available in a forthcoming Bridges preprint.




These are part of a series of temari I have been making. Each one starts as a styrofoam ball, is wrapped in yarn,
then thread, then embroidered with a pattern. This is a craft from Japan (traditionally with a bundle of
cloth instead of the styrofoam core) which originated in China.
In addition to being quite stunning, they are a great avenue to play around with spherical symmetries.
The first two are different Brunnian links, extensions of the Borrommean rings, where if one band is removed,
they all can separate. These designs are based on polyhedra, where each face has a modular structure that combines to
form the link. Specifically, the first has a swirl of three bands for each face of an octahedron, and the second
has a swirl of four bands for each face of the cube. This allows the missing band to propagate, untangling the rest
of the link. I'm planning on also laser cutting wood with these patterns into tiles that you can assemble on a
plane, or latch together into polyhedra. This systems can produce a unique Brunnian link for any polyhedron. I've also
color coded the bands to help evoke the underlying symmetry.
The third ball is a an "orderly tangle" of sorts, a link where each component is a polygon. There are some great
models of these by
George Hart and
also discussed in a book by Alan Holden. I've found making models with plastic straws made into triangles and square is
a good way to play around with these, and have a few as well. This design uses the duality of the color scheme to draw
attention to the dual nature of the octahedron and cube, every vertex of one corresponds to a face of the other.
The pair shows more orderly tangles. The pink and blue color scheme is inverted between the two, as each represent different
ways of interleaving six squares, one for each vertex of an octahedron. The pink base has the sqaures in the orientation of
a cube, whereas the blue base has them rotated 45 degrees. Both designs are overlaid with a tangle of eight triangles,
colored yellow and white to represent the two tetrahedra of a stella octangula. Despite looking different, they are the same
confinguration in each.

These three pieces are made with gemstone beads. Several combinatorial questions are naturally suggested when beading.
For example, how many necklaces of length n can you make with k beads?
Here, the longer bracelet encodes a superpermutation. A superpermutation is a sequence of numbers from the set
1, 2, ..., n whose subsequences of length n give every possible permutation of this set. One could
simply listing all of these, so the challenge is to find the shortest list that does so. This problem was
referenced in a anime, where a character wonders what is the quickest way to watch all 14 episodes of a show in
every order. Following this an anonymous 4chan user proved a novel lower bound on the length of the
shortest superpermutation. This example reminds us that math is all around is if we look, and great insight can
come from anywhere.
Similarly, a DeBrujin sequence ennumerates all strings of some length on a finite alphabet. The necklace
contains all strings of length four in the alphabet a, b, c, represented by the pink, yellow, and purple beads.
These objects can be constructed in a number of fun ways, including finding an Eulerian path in an associated
graph. They have applications to allow a sensor to determine it's position in space (it can read a few bits at its
location, then since each string only appears once, this determines it's location), card tricks, and procedural
generation in video games. As a technical note, DeBrujin sequences are cylic, so it's important the associated
necklace does not have a clasp to disrupt the pattern.
These pieces of artwork can be made interactive by playing a game: pick a random permutation of four elements, for
the first, or string of length four on a three letter alphabet, and try to find it in the piece!
The bracelet is a similar constrained ennumeration. Here it gives all permutations of three elements where adjacent
permutations differ only by swapping two elements. This can also be viewed as trying to find an Eulerian Path in an
associated graph, the permutahedron, and is related to the problem in "Change Ringing" which George Hart has a good
video about on YouTube. An added neat fact is that this constraint means we can represent the sequence are a braid
by drawing three dots for each permutation, and connecting them for each swap. The resulting braid, if connected
back to its start, makes the Borromean rings!
Additionally, each piece is made with the same type of gemstone. Some mineral receive their color from impurities,
and as such they can appear in many colors despite having the same structure. These gems also therefore come in a range of shades (as compared to gems whose color comes from structural
elements, such as peridot). The gemological terms are "allochromatic" and "idiochromatic" respectively.
For example, the necklace and longer
bracelet are made from varieties of quartz: amethyst (purple), citrine (yellow), rose quartz (pink) and smoky quartz
(grey). Silicon dioxide is the most common mineral on earth, and have a variety of gem names for historical reasons.
Quartz can also be translucent, in which case it is called chalcedony, or opaque, in which case it is called jasper
(which also comes in many location-specific forms). The smaller
bracelet is made with three varieties of beryl: aquamarine (blue), morganite (pink) and emerald (green). Jade, calcite,
and common opal are other minerals that come in nearly every color.

This is a cross stitch of a solution to the
Picture Hanging Puzzle, which asks how you can having a picture on n
nails where removing any one nail causes the picture to fall. It is intimately connected to Brunnian links, as
each nail is effectively an unknot in the link. This is a symmetric presentation of a general construction,
where loops can be passed through each other in such a way that they each depend on their neighbors to stay
together. I've also made a wooden version with four removable pegs and a length of rope to tie around them.

This is a mobius ring in sterling silver. Dartmouth College has a truly wonderful jewelry studio where I've had the
pleasure of learning many techniques in my time there. This simple piece was made by twisting a piece of wire and
soldering it together. The mobius band is a well known counterintuitive object: it only has one side despite the
paper it's made from being two sided. It is a very approachable way to introduce some mathematics, as anyone can
make one by taping a twisted strip of paper together. Several topological questions can be asked, for example
how many sides does a similar band have with two, three, four, or more twists? And one of my favorites, what happens
when you cut along the center? In a normal piece of paper, this cuts it into two pieces, but you might be surprised
what happens here!
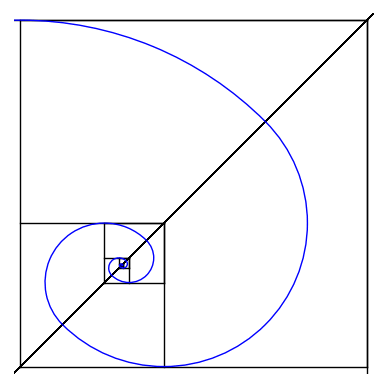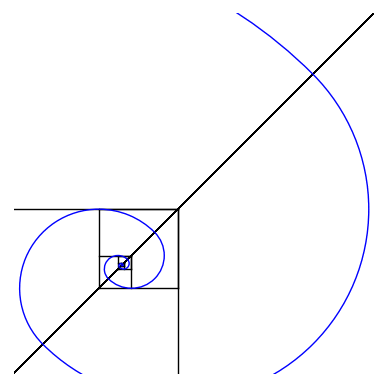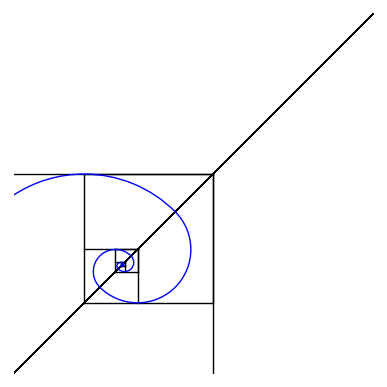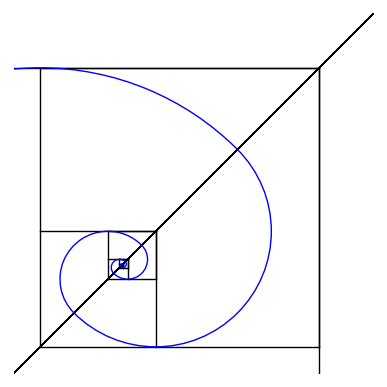
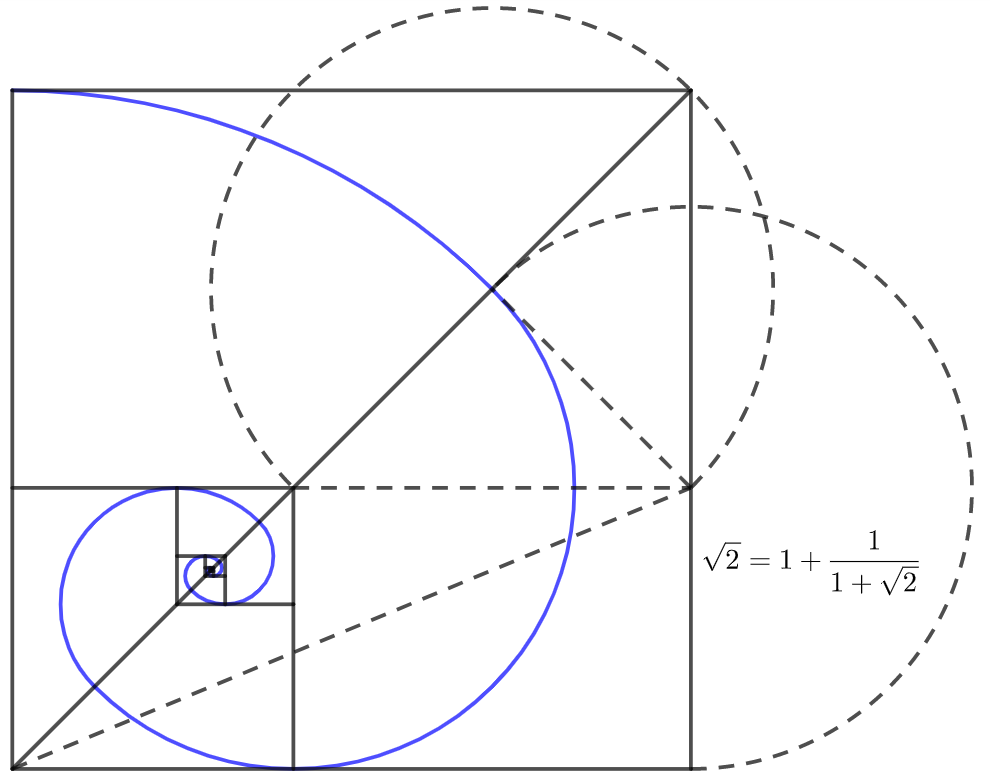
This Gif represents a "proof" that the square root of 2 is irrational. It is a geometric depiction of the fact that
the continued fraction for sqrt(2) is 1/(2+1/(2+1/(2+...))), since x = sqrt(2) satisfies x = 1+1/(1+x). Like a fractal
gif, the nesting of this represents a self-symmetry in the continued fraction. Since it
never terminates, sqrt(2) is not rational. One can think of this as extending Euclid's division algorithm, using each
remainder to divide the next, 1 goes into sqrt(2) once, then the remainder sqrt(2)-1 goes into 1 twice, and so on.
I developed this during my time at the SMALL REU in William's College in the summer 2019 as part of a group project
on continued fractions with Professor Thomas Garrity.
Puzzle Solving and the State Space
Puzzles come in many shapes and forms, but one approach can solve an astounding number of them. By
representing each state of the puzzle as a point in an abstract space, with connections when one can transition
between states with a valid move, one can often find solutions easily. This talk explains this connection in
detail, with several fun examples and puzzles for participants to interact with! If time allows, we’ll also
discuss an amazing result known as the “Sprague-Grundy Theorem” that uses this technique to solve a broad class
of games. If you like puzzles, or get frustrated when you can’t solve them, this talk is for you!
slides.
Probability Paradoxes - Middle and Highschool Summer Math Camp
Along with other graduate students David Freeman, Alina Glaubitz, and Jinman Park, I developed
material for and instructed the Exploring Mathematics Summer camp for middle and high school children in
Summer 2022. One week was on paradoxical results in probability, which I summarized in a
presentation.
Directed Reading Program
Along with Ben Adenbaum, I co-ran the
Dartmouth mathematics DRP in the below terms.
We pair undergraduate students with graduate students and post docs to learn math beyond the standard
curriculum.
- Winter 2023
- Spring 2023, I also supervised Jamison Anderson on a project about mathematical art.
- ...
Hackenbush - Science day 2023
For science day 2023, graduate students Grant Molnar, Kelly Cantwell, and I, along with post doc
Longmei Shu, ran a session on the game Hackenbush for middle and high school students. We made a
handout for students to
complete which explained how to play the game and some of the math behind it. Further references are:
- A website where you can play Hackenbush
interactively and make your own games.
- Two sets of
notes
about the math behind this game.
- A short story
explaining another way to construct the Surreal numbers:
- A Youtube video
explaining this game.
Non-Transitive Dice - Sonia Kovalevsky Day
Most springs Dartmouth runs a fun-filled day of mathematics with hands-on
workshops and talks for middle and high school female students and their
teachers, both women and men. Originally started and funded by the Association
for Women in Mathematics, The purpose of the day is to encourage young women to
continue their study of mathematics and to assist the teachers of female
mathematics students.
In the Spring of 2022, I assisted fellow graduate Yanbing Gu in a presentation on the
four color theorem and its generalizations
to higher genus surfaces realized through crochet.
In the Spring of 2023, I co-led a workshop on mathematical games, presenting on
non-transitive dice.
Students collected data on rolling pairs of dice, seeing there was no best die, then saw the
math
to prove this.


















