Skip to main content

Section 1.7 Going to extremes

Worksheet
A4US

Dartmouth, being in a rural location near the Appalachian Trail as well as the White Mountains, has a lot of opportunity for hiking and climbing. In this exercise, we will use the idea of hiking up a mountain to help us better understand finding the maximum of a function and to translate that understanding into a mathematical technique.

One tool that hikers use is a topographical map. While two-dimensional, these maps have contours on them that show different elevations at different places. By learning to read these maps, hikers can determine routes that meet their objectives: e.g. the fastest route to the top of the mountain or perhaps a route that takes longer but is not as steep.

In this set of exercises, we will think about how we might translate the idea of finding the top of a mountain into mathematical language and develop a technique to solve the problem.

1. Hiking to the peak.

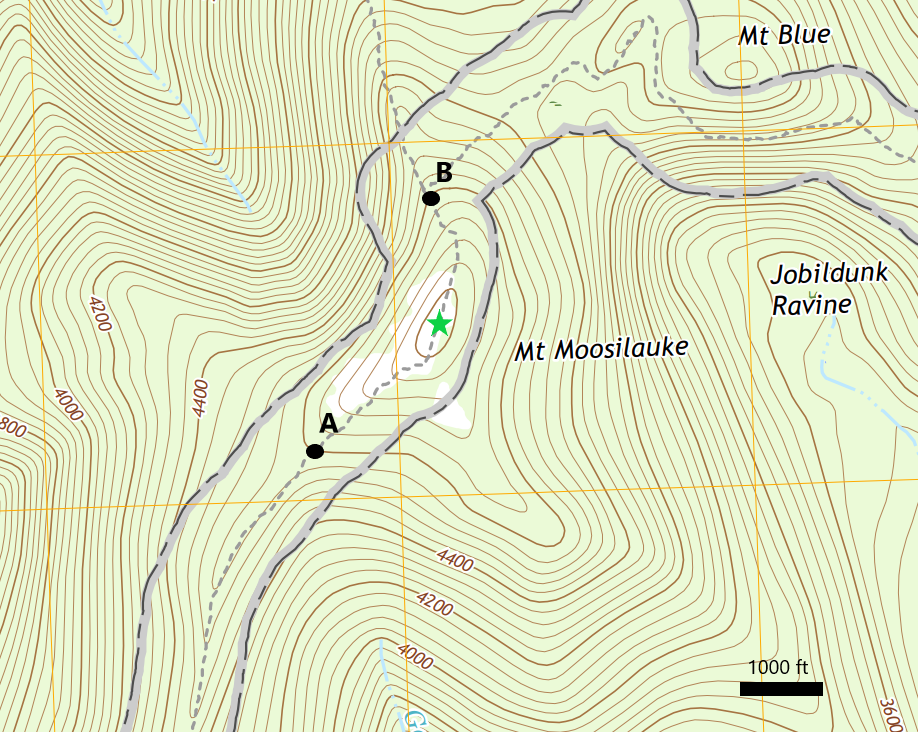
To the right, we have an image of a topographical map that highlights the peak of Mt. Moosilauke. The dotted grey line shows the Appalachian Trail and crosses the peak of Mt. Moosilauke, whihc is marked with a green star.

Imagine yourself walking along the trial and crossing the peak. What are all the ways you might tell if you are at the peak? Brainstorm with your group and make a list of your ideas.

Figure 1.7.1. A section of a topographical map showing the peak of Mt. Moosilauke.
2. Using a function to model the path.

Looking again at Figure 1.7.1, let's focus on the elevation contours. In this map, consecutive contours show a 20 foot gain or loss of altitude. You can estimate the horizontal distance using the scale in the lower right corner showing that one inch on the map is about 1000 feet. Using those contours, plot a rough graph of the elevation as you travel from point \(A\) to point \(B\text{.}\)

A set of axes on the plane to use for plotting the graph of the elevations along the Appalachian Trail.
3. Building a technique to find the peak.

Looking back at your brainstorming list of ways to know you are at the peak, which of them will work well to find the peak just using this sketch? Which won't work? Why not? Discuss these and try to write down a step-by-step algorithm for two or three of your best ideas.

4. Connection to the first derivative test.

Our next step is to take our thinking about finding a peak of a hill and translating it into mathematical language. In the second exercise, you already translated the elevation changes into a functional representation. To formalize this, we will let \(f:I \rightarrow \mathbb{R}\) be a function representing the elevation at different points along the path. The domain of the function, \(I\text{,}\) represents the points on the path between \(A\) and \(B\text{.}\)

Our text provides a definition and a test for the function \(f\) to have an extreme value, like a maximum, at a point in its domain. This first part is the notion of a critical point.

Definition 1.7.2.
Let \(c\) be an interior point in the domain of \(f\text{.}\) We say that \(c\) is a critical point of \(f\) if \(f'(c)=0\) or \(f'(c)\) is undefined.

If we have a critical point, we can further analyze the derivative to classify it using the first derivative test.

The first derivative test: Suppose that \(f\) is a continuous function over an interval \(I\) containing a critical point \(c\text{.}\) If \(f\) is differentiable over \(I\text{,}\) except possibly at point \(c\text{,}\) then \(f(c)\) satisfies one of the following descriptions:

  1. If \(f'\) changes sign from positive when \(x < c \) to negative when \(x>c\text{,}\) then \(f(c)\) is a local maximum of \(f\text{.}\)
  2. If \(f'\) changes sign from negative when \(x < c\) to positive when \(x>c\text{,}\) then \(f(c)\) is a local minimum of \(f\text{.}\)
  3. If \(f'\) has the same sign for \(x < c\) and \(x>c\text{,}\) then \(f(c)\) is neither a local maximum nor a local minimum of\(f\text{.}\)

With your group, look at the algorithms you produced in the previous part. How do they relate to this procedure? Can you perform the same type of translation for your algorithms into mathematical language?