MCMC-based SAR Image Reconstruction
My most recent work has focused on quantifying uncertainty in synthetic aperture radar imaging. Typically in SAR imaging, only a single maximum a posteriori image estimate is retrieved. The maximum is not a categorically strong representative of the posterior, and provides no uncertainty quantification. Instead, we interrogate the posterior by sampling it using a Gibbs sampler. From the samples, confidence intervals are derived for each pixel value. To visualize, we display uniformly random draws from the confidence interval quickly in a gif. Below is a parking lot scene from the GOTCHA SAR data set from Air Force Research Laboratory. We are more confident in persistent features than those that flicker.
 High order total variation Bayesian learning
High order total variation Bayesian learning,
[pdf]
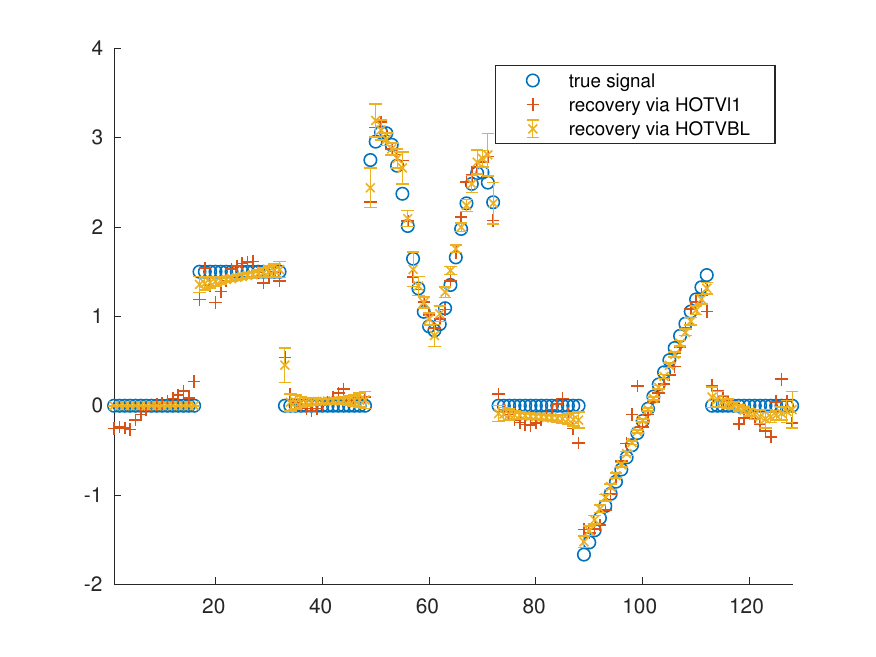
In this project, we modify the total variation operator in order to enable a Bayesian learning algorithm for piecewise smooth function recovery. The paper is submitted to Journal of Scientific Computing.
 Edge detection using sparse Bayesian learning
Edge detection using sparse Bayesian learning,
[pdf]
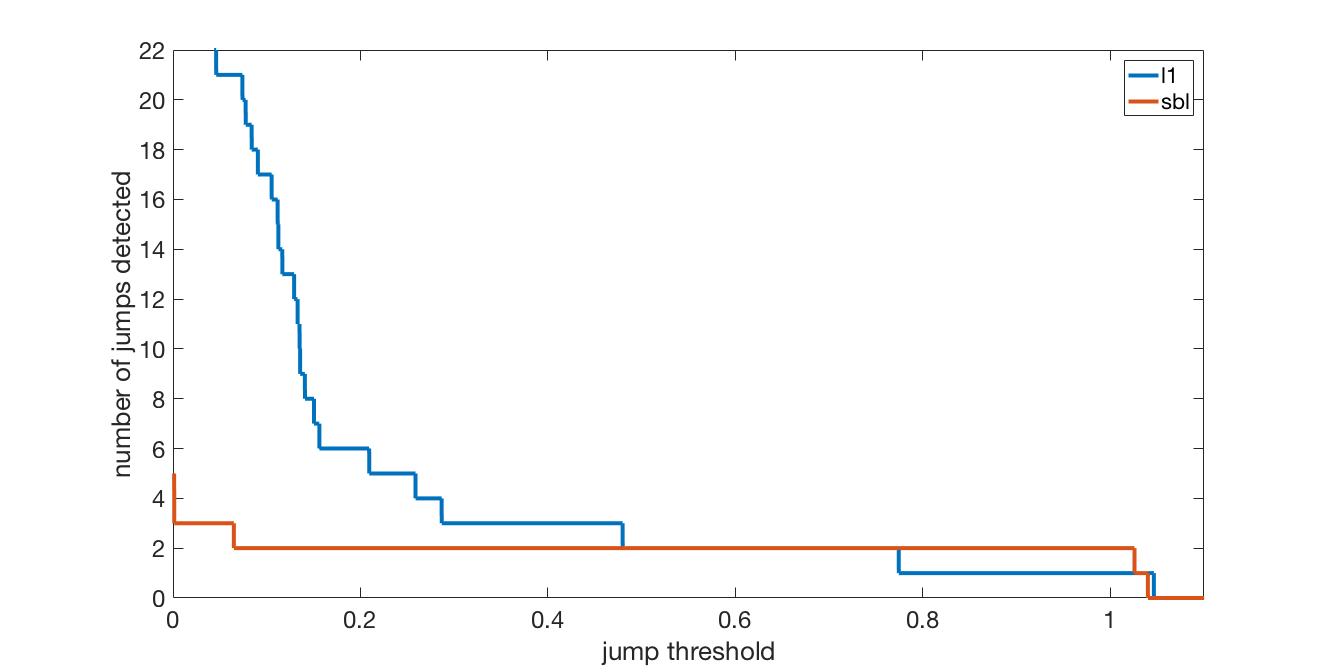
In this project we examine edge detection from non-uniform Fourier data. Below is a comparison of l1 regularization and SBL based on number of jumps detected in a particular problem for a given threshold on the jump height. This plot is derived from the reconstruction of the edge function from logarithmic Fourier sampling with zero-mean Gaussian noise with 0.02 standard deviation. The true number of jumps is two, and we see that SBL correctly identifies this for a wider range of thresholds.
 Binary weighted regularization for edge sparsity
Binary weighted regularization for edge sparsity,
[pdf]
 High order total variation Bayesian learning, [pdf]
In this project, we modify the total variation operator in order to enable a Bayesian learning algorithm for piecewise smooth function recovery. The paper is submitted to Journal of Scientific Computing.
High order total variation Bayesian learning, [pdf]
In this project, we modify the total variation operator in order to enable a Bayesian learning algorithm for piecewise smooth function recovery. The paper is submitted to Journal of Scientific Computing.
 Edge detection using sparse Bayesian learning, [pdf]
In this project we examine edge detection from non-uniform Fourier data. Below is a comparison of l1 regularization and SBL based on number of jumps detected in a particular problem for a given threshold on the jump height. This plot is derived from the reconstruction of the edge function from logarithmic Fourier sampling with zero-mean Gaussian noise with 0.02 standard deviation. The true number of jumps is two, and we see that SBL correctly identifies this for a wider range of thresholds.
Edge detection using sparse Bayesian learning, [pdf]
In this project we examine edge detection from non-uniform Fourier data. Below is a comparison of l1 regularization and SBL based on number of jumps detected in a particular problem for a given threshold on the jump height. This plot is derived from the reconstruction of the edge function from logarithmic Fourier sampling with zero-mean Gaussian noise with 0.02 standard deviation. The true number of jumps is two, and we see that SBL correctly identifies this for a wider range of thresholds.
 Binary weighted regularization for edge sparsity, [pdf]
Binary weighted regularization for edge sparsity, [pdf]