Section 1.9 Continuity
In our examination of limits, we've learned that we can find some limits by simple evaluation but there are others where this doesn't work. Next, we will bring these ideas together through the notion of continuity. Objectives
We have seen that some functions - polynomials and some rational functions - have limits that were easy to find by simply evaluating at the point. We've also seen other functions where we do not have such a simple method. Let's pose the following question - can we find all the functions where we can find limits just through evaluation? In other words, what are all the functions where
How will we go about finding these? Well, let's return to one of our initial examples, \(f(x)=\frac{x^2-4}{x-2}\text{,}\) that we see in Figure 1.9.1. 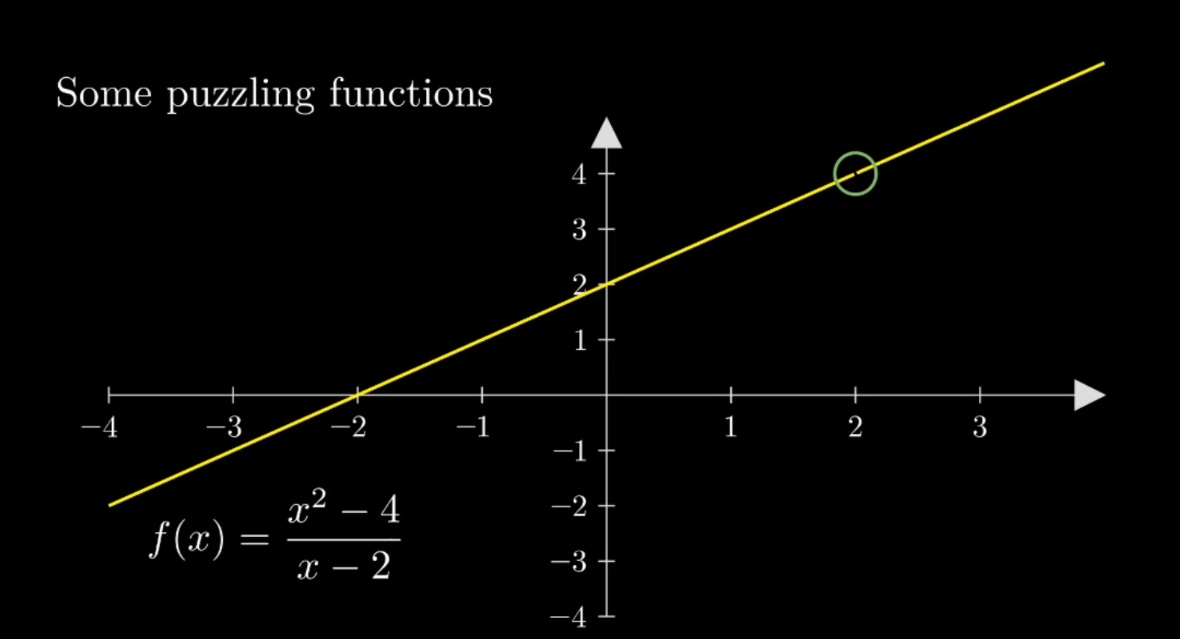
Our second example, \(g(x)=|x-2|/(x-2)\text{,}\) shown in Figure 1.9.2 jumps from minus one to one as we pass through \(x=2\text{.}\) 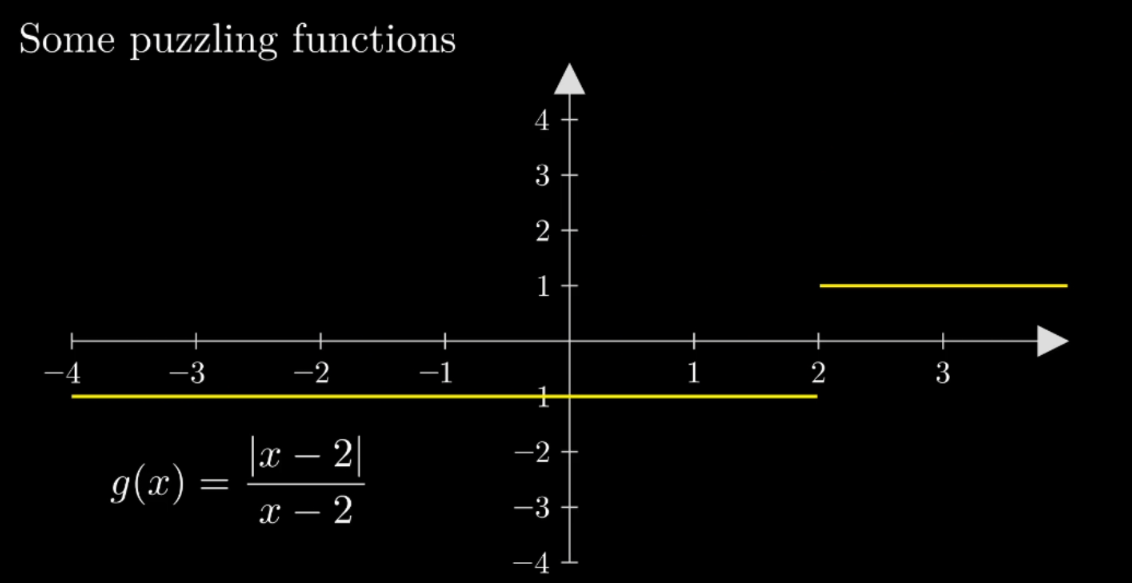
and
Consequently, the limit does not exist as the two one-sided limits do not match. This is a second important property of this set of functions - that the limit at the point exists:
So far we see that we have two conditions - that the function is defined and has a limit at \(a\text{.}\) Is that enough? Let's take a look at a slightly modified version of our first example in Figure 1.9.3. 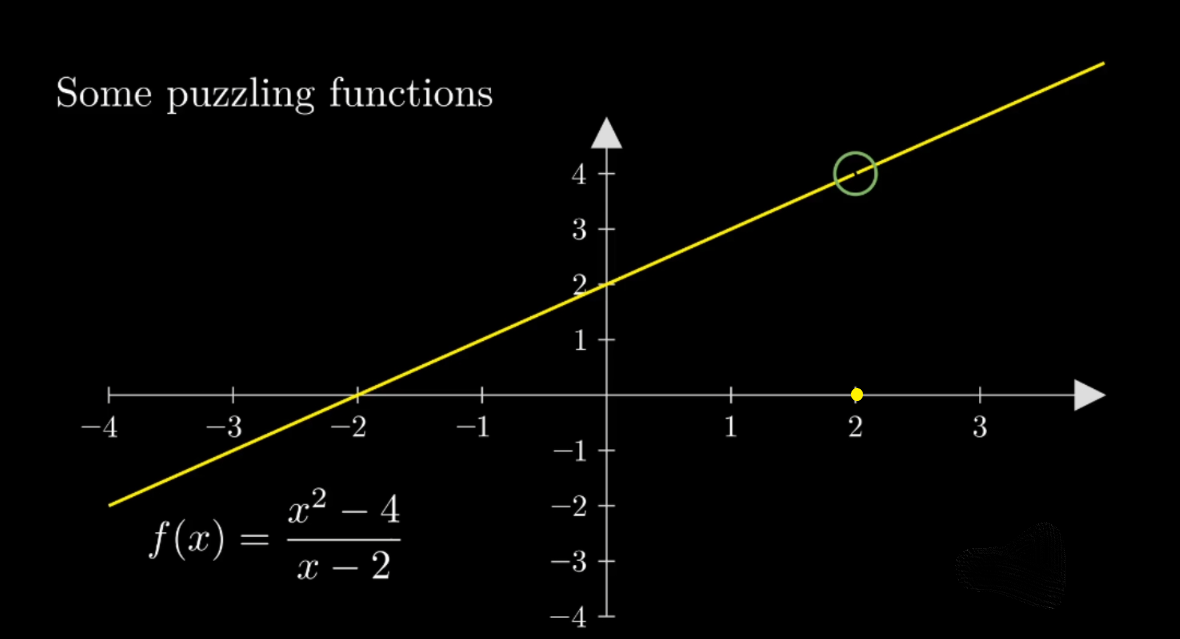
This idea is so useful, we give it a name - a function with this property is continuous at \(x=a\).
Definition 1.9.4.
A function \(f(x)\) is continuous at a point \(a\) if and only if the following three conditions are satisfied:- \(f(a)\) is defined
- \(lim_{x \rightarrow a}f(x)\) exists
- \(\displaystyle lim_{x \rightarrow a}f(x)=f(a)\)
We can now state some of the results of our previous videos using this new language. First, we know that all polynomials are continuous at all points. Second, any rational function is continuous at points in its domain. So long as a rational function is defined at a point, it cannot have a zero in the denominator at there so we can apply the quotient law for limits.
We will also state a fact - there is a proof in the text, but it requires some trigonometric identities we haven't reviewed yet, so we will simply take this as given. The functions sine and cosine are continuous at every point.
We can also name the different types of failures to be continuous and classify discontinuities.
Definition 1.9.5.
If \(f(x)\) is discontinuous at \(a\text{,}\) then
