Skip to main content

Section 1.10 The Intermediate Value Theorem

With the notion of continuity defined, we look at some of its consequences with the intermediate value theorem.

Let's think through some implications of continuity. If we have a function which is continuous over the whole set of real numbers, then if we trace along the curve with a pencil we never need to pick up the pencil to get to the next point on the graph. If we did, there would be some sort of discontinuity.

What consequences does this have? Well, let's think about an example. Suppose we know a few things about \(f(x)\) that we've summarized in the graph in Figure 1.10.1.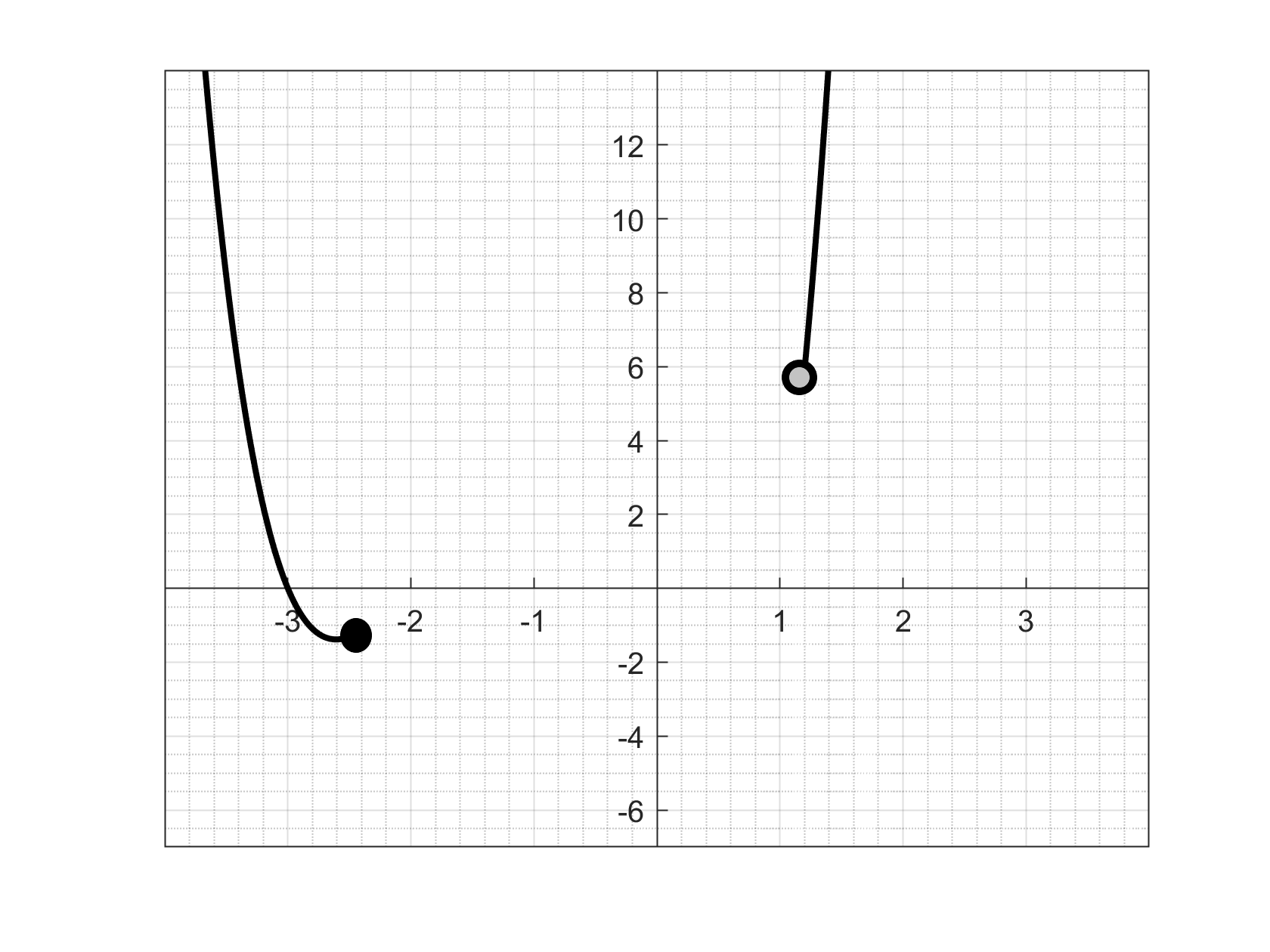

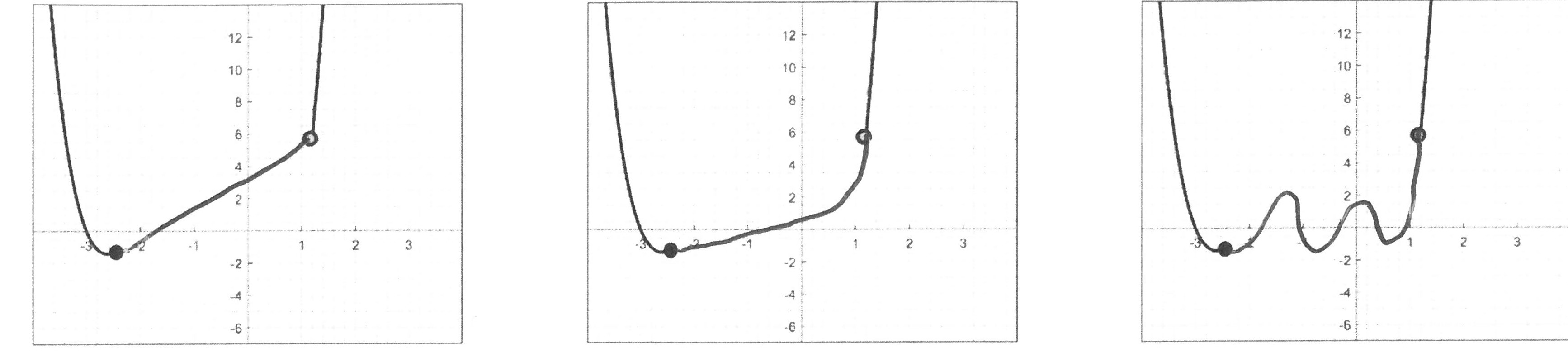
Figure 1.10.1. A partial graph of a function.
We are able to draw a little bit on the left hand side of the graph and a little bit on the right. But what happens in between? If we also know our curve is continuous, the we know that connecting the two pieces means that we have to draw a curve connecting the black point to the grey point without breaks or jumps. So maybe the curve looks like one of the three in Figure 1.10.2, but which one?
Figure 1.10.2. A partial graph of a function with three possible completions.
Well, we don't know - we'd need more information to figure that out. But the fact the we can't pick up our pencil when we draw the curve means that we will pass through every \(y\)-coordinate value between the \(y\)-coordinate of the black point and that of the grey point. We might hit some more than once and we might also hit \(y\)-values outside that range, but we are guaranteed to hit the ones in that range at least once.

The argument we've given is essentially a proof of the intermediate value theorem, which we can state formally.

This idea turns out to be surprisingly useful - it is a way to infer what is happening in parts of the function that you don't know. In this example, one thing we know for sure is that between the black and grey points, the function crosses zero. We don't know where, but we do know that it happens.

Many problems in mathematics can be boiled down to finding zeros. You've seen one version of that problem in finding roots of polynomials, which allows us to break up polynomials into simpler linear factors. Many applied problems work this way too and contribute to experimental design in the sciences. For example, one of the ways neurons communicate with one another is through electrical firing. But how does that work? And how did scientists figure it out? Neuronal firing is mediated by all sorts of things, but is primarily driven by relative the concentration of sodium and potassium ions. To change those concentrations to enable an electrical pulse, potassium is drawn into the cell while sodium is pumped out. But this is hard to observe without very powerful microscopy. But we can use the intermediate value theorem to infer it!

Suppose we measure the sodium and potassium concentrations inside and outside a neuron at two points in time and find, for example, that the sodium level inside the cell at the second time is larger than at the first time. What does this mean? Well, think about a function that models the path of a sodium ion. Our measurement means that at time one some of the sodium atoms were outside the cell, which perhaps we model as a negative value of the function, and that at time two they are inside the cell, which we model as a positive value. Since motion should be continuous, the intermediate value theorem implies that somewhere between time one and time two, the function passes through zero - in other words, the ions pass through the cell membrane. This leads us to the biological hypothesis that there is some mechanism that allows the membrane to be permeable to ion flows.

This example shows us a little bit of the power of mathematical reasoning and the need for abstractions like the notion of continuity. Abstraction allows for two big gains. It lets us to strip away the particulars of a problem and focus on its core features. And, it potentially provides tools that apply to many situations, rather than just one or two.