Geometry | Mathematics at Dartmouth

Geometry is the study of rigid properties of space such as distance, angle and curvature. The surface of the earth, with all its mountains and valleys, is topologically the same as a round sphere but is geometrically very different. A major focus of the geometry group at Dartmouth is Riemannian geometry. Examples of questions addressed by members of the Dartmouth geometry group include:

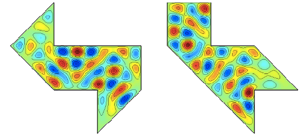
The Inverse spectral problem: How much geometric information about an object is encoded in spectral data? For example, viewing a bounded region in the plane as the surface of an exotically shaped drum, the question appealingly phrased by Mark Kac as “Can one hear the shape of a drum?” asks whether the spectrum of characteristic frequencies of vibration of the drum encodes the shape of the region. We also consider more geometric spectral data such as the “length spectrum”, the collection of lengths of closed geodesics.
The symmetries of a Riemannian manifold form a Lie group. How are the algebraic properties of this Lie group related to the geometry of the Riemannian manifold?

Geometry interacts naturally with nearly every area of mathematics. For example, the inverse spectral problem connects with analysis, combinatorics, group theory and number theory.

Members

Peter Doyle: Hyperbolic geometry
Alena Erchenko: Dynamical systems and ergodic theory; Geometry
Carolyn Gordon: Riemannian geometry, especially spectral geometry and Riemannian homogeneous spaces
Craig Sutton: Riemannian geometry, especially spectral geometry and Riemannian homogeneous spaces
David Webb: Differential geometry; K-theory

Activities

Geometry Seminar