Mathematics ... It's not high school anymore!
The Department of Mathematics gives special attention not only to the future mathematician, computer scientist, physical scientist, and engineer, but also to students who primary interests are in the humanities or social sciences. The department recognizes that knowledge in the mathematical sciences is essential in many disciplines.
Below we attempt to give some guidance to people choosing their first few mathematics courses at Dartmouth. Beyond these initial courses, interested students should feel free to contact one of the department advisors to majors and minors.
More complete descriptions of the courses mentioned below are available in the ORC pages online.
Recommendations based upon interests and backgrounds
Non-calculus options with no prerequisites
What are non-calculus options after Math 8
Courses for students with advanced preparation
The core calculus track

- Course nodes which are located above other nodes are prerequisite. Your entry point may be affected by your advanced placement (See the AP info page).
- Math 1 is an introduction to single variable calculus for students who have not taken calculus before. It is offered Fall term only.
- Math 3 This course is an introduction to single variable calculus aimed at students who have seen some calculus before, either before matriculation or in Math 1. It is offered Fall and Winter terms only.
- Math 8 This course is a sequel to MATH 3 and is appropriate for students who have successfully completed an AB calculus curriculum (or the equivalent) in secondary school. Roughly half of the course is devoted to topics in one-variable calculus, and the second half of the course studies scalar valued functions of several variables. It is offered Fall, Winter, and Spring terms.
- Math 13 This course is a sequel to Math 8 and provides an introduction to calculus of vector-valued functions. It is offered Fall, Winter and Spring terms.
Advanced placement options
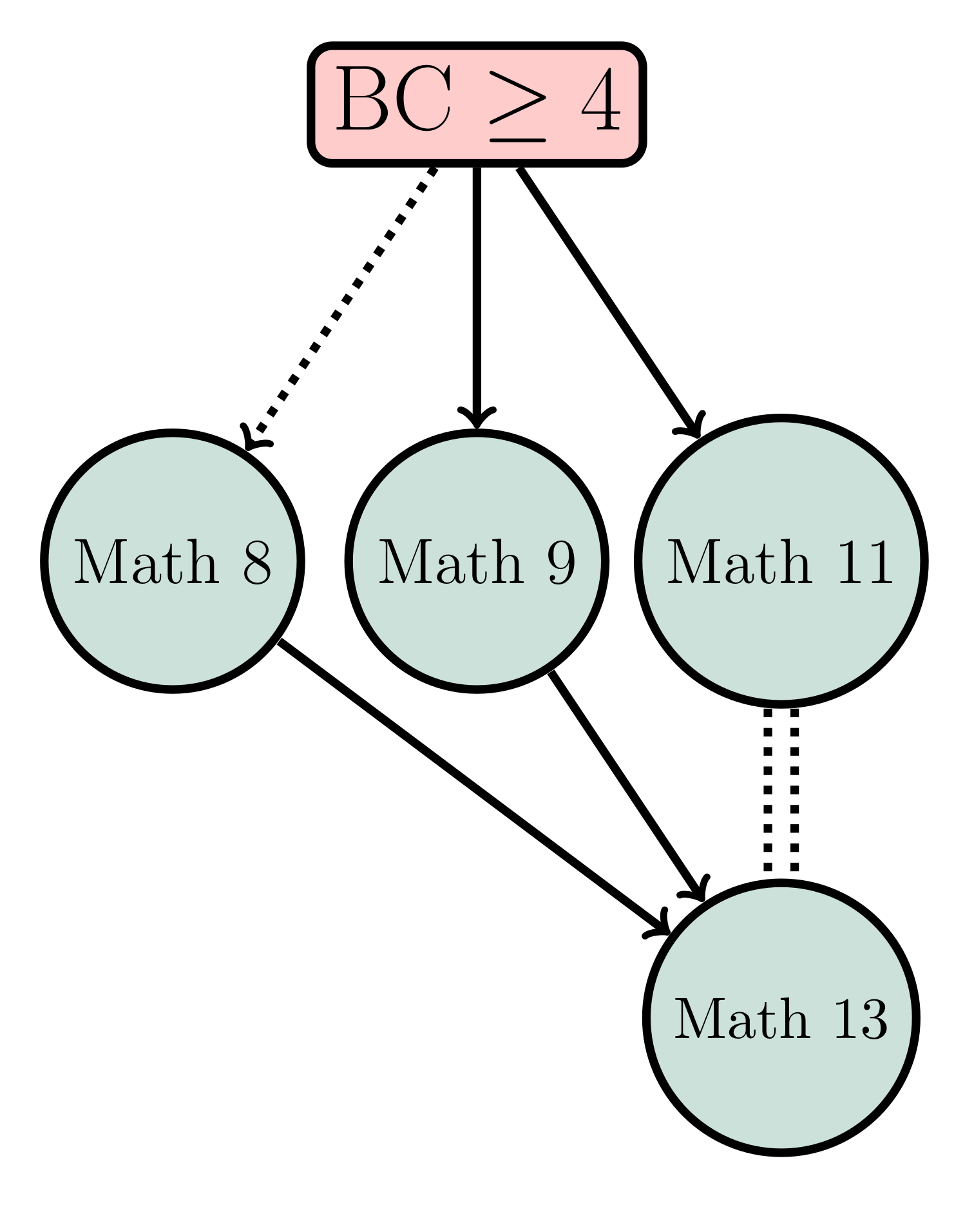
- These courses are options only for those with an AP score on the BC exam of a 4 or 5.
- Math 8 If you are rather tentative about your skills on the later parts of the BC syllabus, e.g., techniques of integration and infinite series, you could (even though you officially have credit for it), opt to (re)take Math 8 (Calculus of Functions of One and Several Variables). This option offers a chance to strengthen areas from the BC syllabus in the first half of the course, while then advancing to introduce the differential multivariable calculus. It is offered Fall, Winter, and Spring terms.
- Math 9 If you are confident in your knowledge of the BC syllabus material (so do not want to repeat it), yet want to move forward at a less brisk pace than offered by Math 11, the course Math 9 (Multivariable Differential Calculus with Linear Algebra) is for you. It offers the material from the second half of Math 8, but enhanced with a brief introduction to linear algebra so as to better explain how derivatives of functions of several variables are linear approximations to functions. Following Math 9, the next course in the calculus sequence would be Math 13. Fall term only.
- Math 11 If you are very confident in your knowledge of material on the BC syllabus, and are up for a briskly paced course, then Math 11 (Calculus for students with two terms of advanced placement credit) would be a good choice for you. This course covers the material from the second half of Math 8 on the differential aspects of multivariable calculus, while also covering the integration theory of Math 13. At the end of this course, you will have the equivalent of Math 13, and can take any course for which Math 13 is listed as a prerequisite. Fall term only.
Non-calculus options with no prerequisites
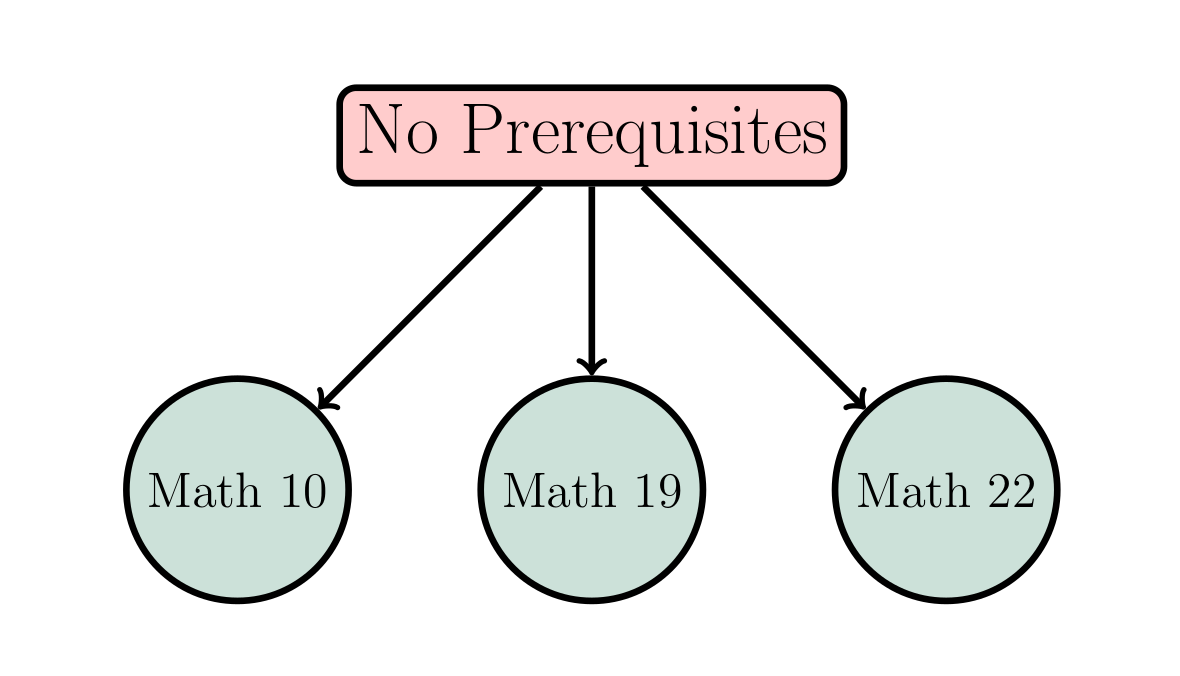
- Math 10 Introductory Statistics. An introduction to the basic concepts of statistics. Topics include elementary probability theory, descriptive statistics, the binomial and normal distributions, confidence intervals, basic concepts of tests of hypotheses, chi-square tests, nonparametric tests, normal theory t-tests, correlation, and simple regression. Packaged statistical programs will be used. Spring term only.
- Math 19 Introduction to Set Theory. This course introduces the axioms of set theory, the universe of sets, and set theory as a foundation for mathematics. It touches on historical and philosophical aspects of set theory. Mathematical topics covered include the algebra of sets, ordinals and cardinals, transfinite induction and recursion, and the axiom of choice. Students will learn language and concepts used throughout mathematics, and learn how to write mathematical proofs. Spring term only.
- Math 22 Linear Algebra with Applications. This course presents the fundamental concepts and applications of linear algebra with emphasis on Euclidean space. Significant goals of the course are that the student develop the ability to perform meaningful computations and to write accurate proofs. Students who plan to take either Math 63 or Math 71 are strongly encouraged to take Math 24 instead of Math 22. Fall, Winter, and Spring.
Non-calculus options after Math 8
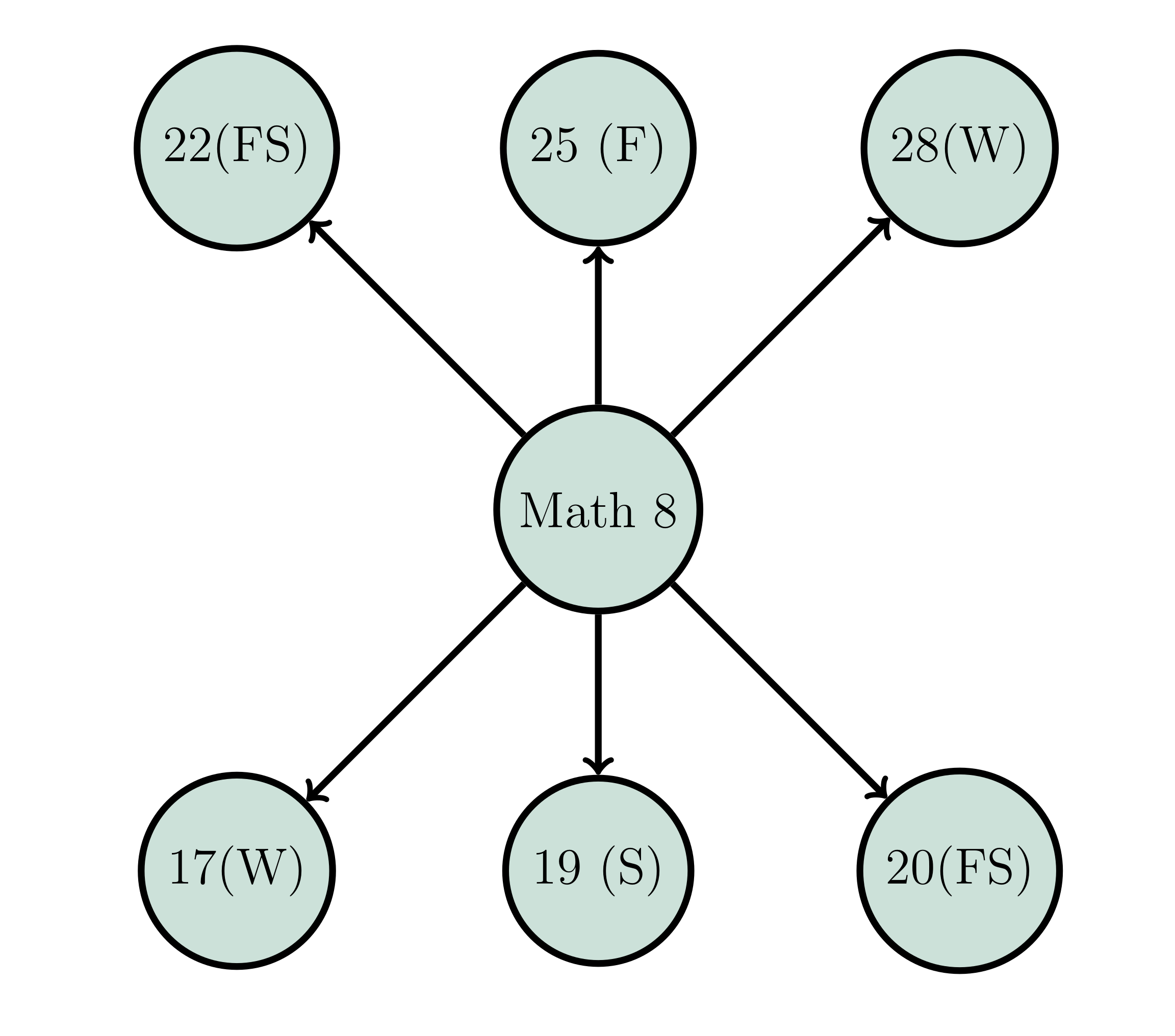
- Math 17 An introduction to Mathematics Beyond Calculus. Gives prospective Mathematics majors an early opportunity to delve into topics outside the standard calculus sequence. Specific topics will vary from term to term, according to the interests and expertise of the instructor. Designed to be accessible to bright and curious students who have mastered BC Calculus, or its equivalent. This course counts toward the Mathematics major, and is open to all students, but enrollment may be limited, with preference given to first-year students. It is offered Winter and Spring terms.
- Math 19 Introduction to Set Theory. This course introduces the axioms of set theory, the universe of sets, and set theory as a foundation for mathematics. It touches on historical and philosophical aspects of set theory. Mathematical topics covered include the algebra of sets, ordinals and cardinals, transfinite induction and recursion, and the axiom of choice. Students will learn language and concepts used throughout mathematics, and learn how to write mathematical proofs. Spring term only.
- Math 20 Probability. This course will serve as an introductions to the foundations of probability theory. Topics covered will include some of the following: (discrete and continuous)random variable, random vectors, multivariate distributions, expectations; independence, conditioning, conditional distributions and expectations; strong law of large numbers and the central limit theorem; random walks and Markov chains. There is an honors version of this course: see MATH 60. Fall and Spring.
- Math 22 Linear Algebra with Applications. This course presents the fundamental concepts and applications of linear algebra with emphasis on Euclidean space. Significant goals of the course are that the student develop the ability to perform meaningful computations and to write accurate proofs. Students who plan to take either Math 63 or Math 71 are strongly encouraged to take Math 24 instead of Math 22. Fall and Spring.
- Math 25 Number Theory. Number theory is that part of mathematics dealing with the integers and certain natural generalizations. Topics include modular arithmetic, unique factorization into primes, linear Diophantine equations, and Fermat's Little Theorem. Discretionary topics may include cryptography, primality testing, partition functions, multiplicative functions, the law of quadratic reciprocity, historically interesting problems. Fall term only.
- Math 28 Introduction to Combinatorics. Beginning with techniques for counting-permutations and combinations, inclusion-exclusion, recursions, and generating functions-the course then takes up graphs and directed graphs and ordered sets, and concludes with some examples of maximum-minimum problems of finite sets. Topics in the course have application in the areas of probability, statistics, and computing. Winter term only.
Advanced options
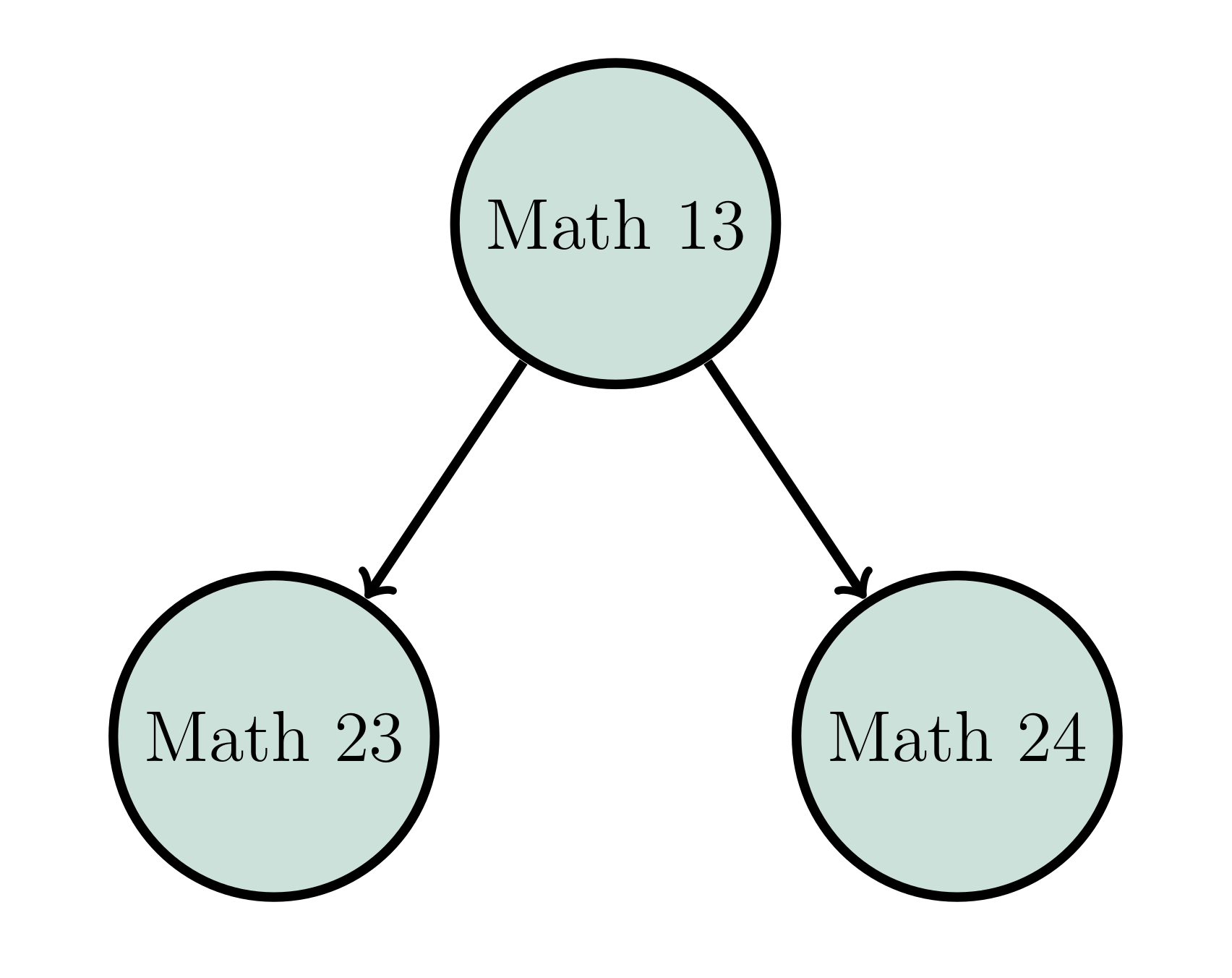
- Math 23 Differential Equations. It is offered in fall, winter, and spring terms. This course is a survey of important types of differential equations, both linear and non-linear. Topics include the study of systems of ordinary differential equations using eigenvectors and eigenvalues, numerical solutions of first and second order equations and of systems, and the solution of elementary partial differential equations using Fourier series. Fall, Winter, and Spring terms.
- Math 24 Linear Algebra. This course is an introduction to the fundamental concepts of linear algebra in abstract vector spaces. The topics and goals of this course are similar to those of Math 22, but with an additional emphasis on mathematical abstraction and theory. (Math 24 can be substituted for Math 22 as a prerequisite for any course or program, but is the preferred option for those pursuing a major in pure mathematics.) Winter and Spring terms only.

