- Structure of this thesis
- Chapters 2,3 and 4: Dissipation rate and deformations of chaotic billiards
- Chapters 5 and 6: Improved billiard quantization methods
- Chapter 7: Quantum point contact conductance and scattering in the half-plane
- Chapter 8: Waveguides for neutral atoms using evanescent light fields
- Review of classical dissipation in a general system
- Review of the linear response theory of quantum dissipation
- Quantum-classical correspondence
- The cavity system
- The white noise approximation (WNA)
- `Special' deformations
- The WNA revisited--cavity shape effects
- Introduction and history of quantum eigenproblems
- Definition of the billiard problem
- Representation by a Helmholtz basis
- The choice of norm matrix
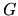
- The hunt for local tension minima as a function of
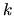
- Conclusion and discussion
- The basic scaling method
- Higher-order correction and normalization
- Sources of error in the method
- Application: local density of states at finite deformations
- Discussion
- Conductance in terms of cross section
- Partial-wave channel modes for a 2-terminal system
- Idealized `slit' aperture point contact
- Point contact coupled to a resonator
- What is the maximum conductance of a single quantum channel?
- Reciprocity and `conductance' of atom waves
- Conclusions
- Introduction
- Trap Concept
- Trap properties
- Numerical solution of the light fields
- Further decoherence and loss mechanisms
- Conclusion
- Trajectories--the issue of exponential divergence
- General system--windowed estimation of correlation spectrum
- Considerations in a billiard system
- Expansion of the dilation operator
- Curvilinear boundary coordinates
- Applying boundary conditions and simplifying
- Tension matrix expansion
- Useful geometric boundary integrals
- Basis `badness'
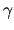
- Real plane waves (RPWs)
- Adding evanescent plane waves (EPWs)
- Symmetrization and reduction of effort